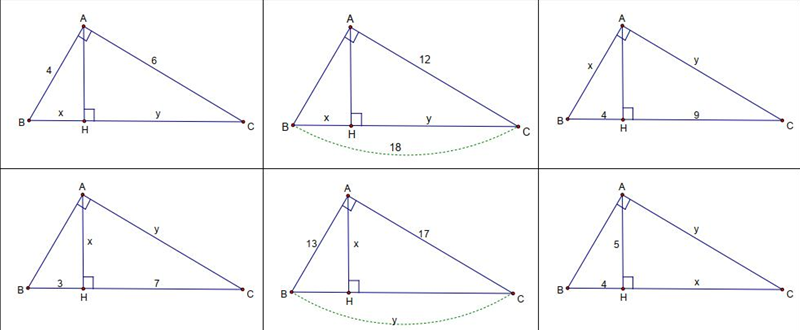
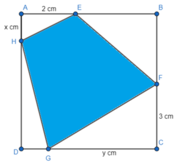
Tìm x,y trong hình vẽ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: BC = BH + HC = y + 32
Áp dụng hệ thức lượng A B 2 = B H . B C trong tam giác vuông ABC ta có:
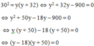
⇔ y − 18 = 0 y + 50 = 0 ⇔ y = 18 N y = − 50 L
Suy ra y = 18 => BC = 18 + 32 = 50
Áp dụng hệ thức lượng A C 2 = C H . B C ta có:
![]()
Vậy c = 40; y = 18
Đáp án cần chọn là: D

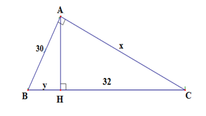
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
A B 2 = B H . B C ⇔ B H = A B 2 B C = 144 20 = 7 , 2 => CH = BC – BH = 20 – 7,2 = 12,8
Vậy x = 7,2; y = 12,8
Đáp án cần chọn là: C

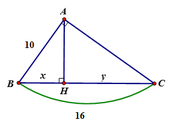
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
A B 2 = B H . B C ⇔ B H = A B 2 B C = 100 16 = 6 , 25 => CH = BC – BH = 16 – 6,25 = 9,75
Vậy x = 6,25; y = 9,75
Đáp án cần chọn là: B


Ta có:
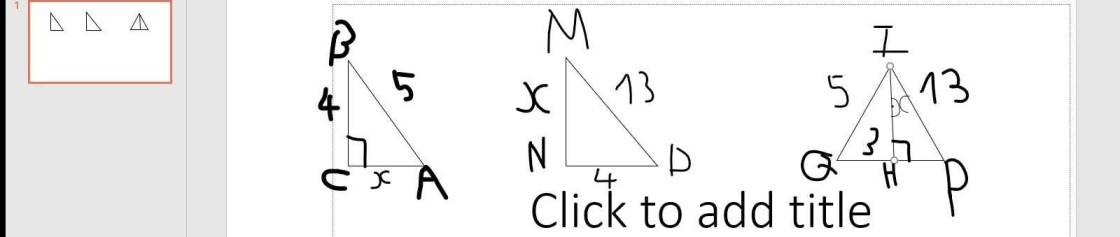
\(\Delta ABC\) vuông tại \(C\)
\(\Rightarrow AC^2+BC^2=AB^2\left(Pytago\right)\)
\(\Rightarrow x^2+4^2=5^2\\ \Leftrightarrow x=\sqrt{5^2-4^2}\\\Leftrightarrow x=3 \)
Ta có : \(\Delta MND\) Vuông tại N
\(\Rightarrow MN^2+ND^2=MD^2\left(Pytago\right)\\ \Rightarrow x^2+4^2=13^2\\ \Leftrightarrow x=\sqrt{13^2-4^2}\\ \Leftrightarrow x=3\sqrt{17}\)
Xét \(\Delta QIH\) vuông tại H:
\(QH^2+IH^2=QI^2\left(Pytago\right)\\ \Rightarrow3^2+x^2=5^2\\ \Leftrightarrow x=\sqrt{5^2-3^2}\\ \Leftrightarrow x=4\)


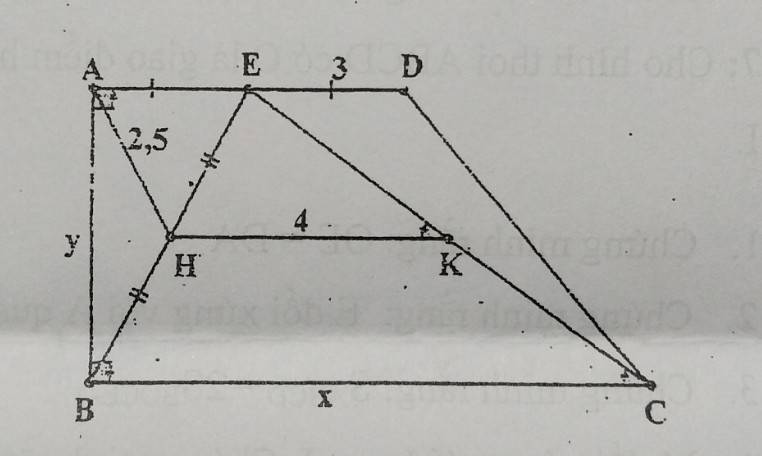
Có: ∠EKH = ∠KCB
Mà 2 góc ở vị trí đồng vị
⇒ HK // BC
Xét △EBC có:
H trung điểm EB
HK // BC
⇒ HK đường trung bình
⇒ HK = \(\dfrac{1}{2}\)BC
⇒ BC = 2HK
⇒ x = 2 . 4 = 8
Xét △AEB ⊥ A, có:
AH đường trung tuyến (H trung điểm EB)
⇒ AH = \(\dfrac{1}{2}\)EB
⇒ EB = 2AH = 2 . 2,5 = 5
Vì AE = ED
Mà ED = 3
⇒ AE = 3
Áp dụng định lý Pytago vào △AEB ⊥ A
⇒ \(EB^2=AE^2+AB^2\)
⇒ AB = y = \(\sqrt{BE^2-AE^2}\) = \(\sqrt{5^2-3^2}\) = \(4\)
Vậy x = 8 và y = 4

Chọn C.
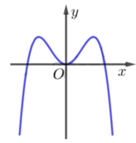
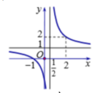
Từ đồ thị dễ thấy hàm số nghịch biến và liên tục trên [-3;0] nên m a x [ - 3 ; 0 ] f ( x ) = f(-3)
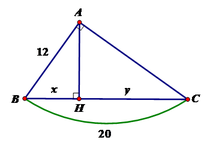

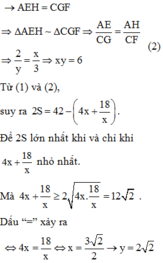
\(\Delta ABC\)vuông tại A, đường cao AH \(\Rightarrow AH^2=BH.CH\left(htl\right)\)
\(\Rightarrow CH=\frac{AH^2}{BH}=\frac{6^2}{3}=12\)hay x = 12
\(\Delta ACH\)vuông tại H \(\Rightarrow AC^2=AH^2+CH^2\left(đlPytago\right)\)
\(\Rightarrow AC^2=6^2+12^2=36+144=180\)
\(\Rightarrow AC=\sqrt{180}=6\sqrt{5}\)hay \(y=6\sqrt{5}\)