Cho đường tròn (C) có phương trình x − a 2 + y − b 2 = R 2 và điểm M ( x 0 ; y 0 ) nằm bên trong đường tròn. Đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB. Phương trình của ∆ là:
A. ( a - x 0 ) ( x - x 0 ) + ( b - y 0 ) ( y - y 0 ) = 0
B. a + x 0 x − x 0 + b + y 0 y − y 0 = 0
C. ( a - x 0 ) ( x + x 0 ) + ( b - y 0 ) ( y + y 0 ) = 0
D. a + x 0 x + x 0 + b + y 0 y + y 0 = 0

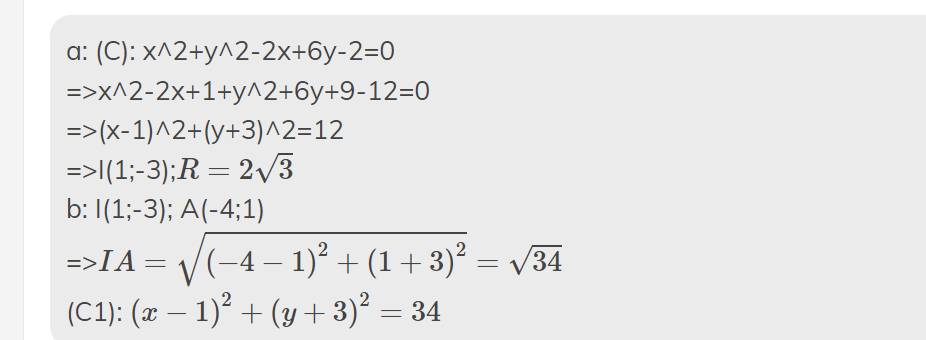
Đáp án A.
Đường tròn (C) có tâm I(a;b).
Theo quan hệ vuông góc đường kính và dây cung: Nếu đường thẳng ∆ qua M cắt đường tròn tại hai điểm A, B sao cho M là trung điểm của AB thì ∆ ⊥ I M tại M.
Do đó, đường thẳng ∆: đi qua M x 0 ; y 0 và nhận M I → = a - x 0 ; b - y 0 làm VTPT.
Phương trình ∆: a - x 0 x - x 0 + b - y 0 y - y 0 = 0