Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Xét ΔBNC có
CI,BK là đường cao
CI cắt BK tại E
Do đó: E là trực tâm của ΔBNC
=>NE\(\perp\)BC
mà AB\(\perp\) BC
nên NE//AB
Xét ΔKAB có
N là trung điểm của KA
NE//AB
Do đó; E là trung điểm của BK
=>EB=EK
a: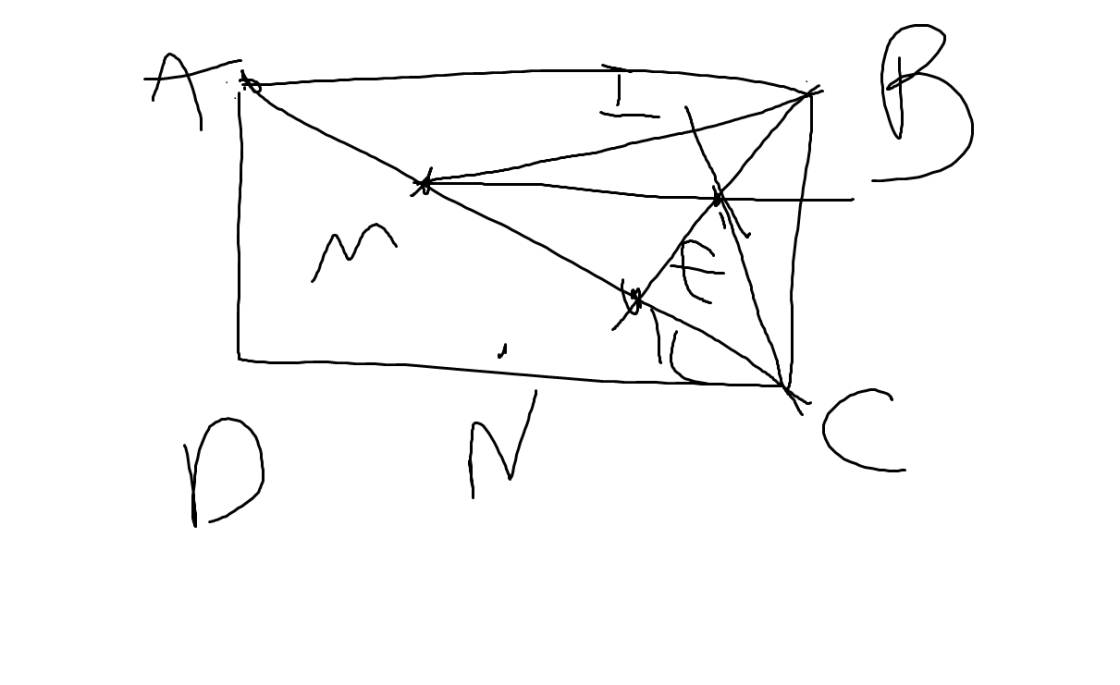 
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
a) ∆MBC có hai đường cao BP và CQ cắt nhau tại E nên E là trực tâm của tam giác => ME là đường cao thứ ba => ME⊥BC (đpcm)
b) ABCD là hình chữ nhật (1) nên AB⊥BC kết hợp với ME⊥BC => ME // AB (2) mà M là trung điểm của AP nên E là trung điểm của BP => ME là đường trung bình của ∆APB => ME = 1/2AB và NC = 1/2CD (gt) nên ME = NC (do AB = CD)
Từ (1) và (2) suy ra ME//NC
Tứ giác MNCE có ME = NC và ME//NC nên là hình bình hành
c) Tứ giác MNCE là hình bình hành nên ^NMC = ^MCE
Mà ^MCE + ^CMQ = 900 (∆MCQ vuông tại Q) nên ^NMC + ^CMQ = 900 => NMQ = 900 => BM vuông góc với MN (đpcm)
Chọn B.
Xét đáp án B
Đặt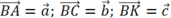
và BA = a; BC = b và BK = c.
Do M là trung điểm của AK nên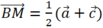
,
Do đó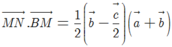
Vì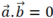
và 
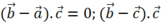nên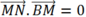 
Suy ra MN và BM vuông góc với nhau
Do đó góc BMN bằng 900.