Cho tứ diện ABCD và ba điểm P,Q,R lần lượt nằm trên cạnh AB, CD, BC; biết PR//AC. Xác định giao tuyến của hai mặt phẳng (PQR) và (ACD) là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
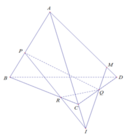
Ta có: PR ∩ AC = I
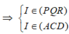
Xét (PQR) và (ACD) có:
I là điểm chung
Q là điểm chung
⇒ Giao tuyến chủa (PQR) và (ACD) là QI

Đáp án D

Xét (PQR) và (ACD) có:
Q là điểm chung
PR // (ACD) ( do PR // AC)
⇒ giao tuyến của 2 mặt phẳng là đường thẳng d đi qua Q và song song PR
d cắt AD tại điểm S cần tìm
⇒ SQ // AC
Mà Q là trung điểm CD
⇒ S là trung điểm AD

Đáp án A
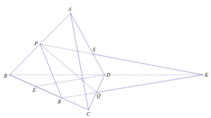
Xét (BCD) có: RQ ∩ BD = K
⇒ K ∈ (ABD)
Xét (ABD) có: PK ∩ AD = S
Gọi E là trung điểm BR
⇒ R là trung điểm đoạn EC
Mà Q là trung điểm CD
⇒ RQ là đường trung bình tam giác DEC
⇒ RQ // DE ⇒ RK // DE
Xét tam giác BRK có: RK // DE và E là trung điểm BR
⇒ D là trung điểm BK
Xét tam giác ABK có: AD là đường trung tuyến cạnh BK
và KP là đường trung tuyến cạnh AB
PK ∩ AD = S
⇒ S là trọng tâm tam giác ABK
⇒ S A S D = 2
Đáp án C
Xét (PQR) và (ACD) có:
Q là điểm chung
AC // PR
⇒ giao tuyến (PQR) và (ACD) là Qx song song với AC