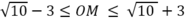Cho số phức z thỏa mãn 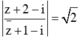. Tìm giá trị nhỏ nhất và giá trị lớn nhất của modul z lần lượt là. ...
Đọc tiếp
Cho số phức z thỏa mãn 
. Tìm giá trị nhỏ nhất và giá trị lớn nhất của modul z lần lượt là.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 10 2019
Đáp án B
z = x + y i , ( x , y ∈ ℝ ) ⇒ P = x + 2 2 + y 2 − x 2 - y - 1 2 = 4 x + 2 y + 3 z − 3 − 4 i = 5 ⇔ x - 3 2 + y - 4 2 = 5
Đặt x = 3 + 5 sin t , y = 4 + 5 cost thỏa mãn ( x − 3 ) 2 + ( y − 4 ) 2 = 5
CM
5 tháng 7 2019
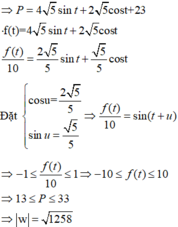
Đáp án B
z = x + y i , ( x , y ∈ R ) ⇒ P = x + 2 2 + y 2 - x 2 - y - 1 2 = 4 x + 2 y + 3 z - 3 - 4 i = 5 ⇔ x - 3 2 + y - 4 2 = 5
Đặt x = 3 + 5 sin t , y = 4 + 5 cos t thỏa mãn x - 3 2 + y - 4 2 = 5
⇒ P = 4 5 sin t + 2 5 cos t + 23 f t = 4 5 sin t + 2 5 cos t f t 10 = 2 5 5 sin t + 5 5 cos t
Đ ặ t c o s u = 2 5 5 sin u = 5 5 ⇒ f t 10 = sin t + u ⇒ - 1 ≤ f t 10 ≤ 1 ⇒ - 10 ≤ f t ≤ 10 ⇒ 13 ≤ P ≤ 33 ⇒ w = 1258
CM
7 tháng 12 2018
Đáp án B.
Đặt z = x + y i x , y ∈ ℝ suy ra tập hợp các điểm M(z) = (x,y) là đường tròn (C) có tâm I(3;4) và bán kính R = 5 .
Ta có P = z + 2 2 - z - i 2 = x + 2 + y i 2 - x + y - 1 i 2 = x + 2 2 + y 2 - x 2 - y - 1 2
= x 2 + y 2 + 4 x + 4 - x 2 - y 2 + 2 y - 1 = 4 x + 2 y + 3 → ∆ : 4 x + 2 y + 3 - P = 0 .
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung ⇔ d I ; ∆ ≤ R .
⇔ 4 . 3 + 2 . 4 + 3 - P 4 2 + 2 2 ≤ 5 ⇔ 23 - P ≤ 10 ⇔ - 10 ≤ 23 - P ≤ 10 ⇔ 13 ≤ P ≤ 33 .
Do đó, m a x P = 33 m i n P = 13 → w = M + m i = 33 + 13 i ⇒ w = 1258 .
Chọn A.
Giả sử z = x + yi. Từ giả thiết:
Suy ra: ( x + 2) 2+ ( y - 1)2 = 2[(x + 1) 2 + ( y + 1) 2]
Hay x2 + (y + 3)2 = 10
Tập hợp điểm biểu diễn của z là đường tròn tâm I(0; -3) bán kính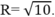
Gọi M là điểm biểu diễn của z, ta có:
IM-IO ≤ OM ≤ IM+ IO hay