Cho số phức z thỏa mãn ![]() là một số thực. Hỏi giá trị nhỏ nhất của |z| gần với giá trị nào nhất?
là một số thực. Hỏi giá trị nhỏ nhất của |z| gần với giá trị nào nhất?
A. 2.7
B. 2.8
C. 1,3
D. 1,4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Đặt z = x+ yi.
Khi đó
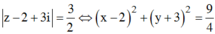
Các điểm M biểu diễn số phức z thỏa mãn hệ thức đã cho nằm trên đường tròn tâm I(2;-3) và bán kính R = 3/2.
Ta có: min|z| khi và chỉ khi M nằm trên đường tròn và gần O nhất.
Đó là điểm M1( là giao điểm của tia IO với đường tròn) (Bạn đọc tự vẽ hình).
Ta có: ![]() . Kẻ
. Kẻ ![]()
Theo định lý talet ta có:
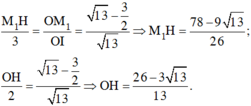
Vậy 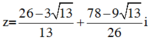

Chọn C.
Ta có |z|2 + |(z – 1 – 2i) + (1 + 2i)|2 = |z – 1- 2i|2 + |1 + 2i|2 + 2(z – 1 – 2i)(1 + 2i) (1)
|z – 3 – 6i|2 = |(z – 1 – 2i) – 2(1 + 2i)|2 = |z – 1 – 2i|2 + 4|1 + 2i|2 - 4(z – 1- 2i)(1 + 2i) (2)
Từ (1) và (2) suy ra: 2|z|2 + |z – 3- 6i|2 = 3|z – 1- 2i|2 + 6|1 + 2i| = 12 + 30 = 42.
Áp dụng bất đẳng thức Bunhiakovsky ta có:

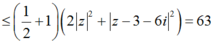
![]()
Vậy ![]()

Chọn đáp án B.
Cách 1: (Sử dụng kiến thức Hình học)
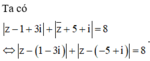
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức
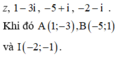
Có I là trung điểm của đoạn thẳng AB và

Áp dụng bất đẳng thức Cô-si, ta có


Cách 2: (Sử dụng kiến thức Đại số)
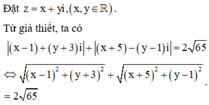
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có
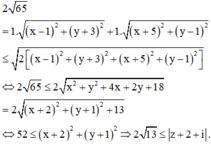
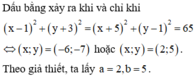


Đáp án A
Gọi z = x + i y , x , y ∈ ℝ
z - 1 - i = 1 ⇔ x + i y - 1 - i = 1
⇔ x - 1 2 + y - 1 2 = 1 2 C
Gọi I là tâm của đường tròn (C).
Với mọi điểm P bất kì chạy trên S,
ta có O P ≤ O M + M P
do đó số phức tương ứng với P có môđun lớn nhất
khi và chỉ khi OP lớn nhất
OP = OM + MP
Tương đương 3 điểm O, M, P thẳng hàng
và M nằm giữa O và P
⇔ P ≡ P ' x P > 1
Phương trình đường thẳng OI: y = x
Tọa độ P’ là nghiệm của hệ phương trình :

Chọn B.
Giả sử z = x + yi.
Từ giả thiết: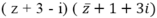 = ( x + 3 + ( y - 1) i) ( x + 1 - ( y - 3) i)
= ( x + 3 + ( y - 1) i) ( x + 1 - ( y - 3) i)
= x2 + y2 + 4x + 4y + 6 + 2( x – y - 4) i
Để số trên là 1 số thực khi và chỉ khi : x – y – 4 = 0
Tập hợp biểu diễn của z là đường thẳng d: x – y – 4 = 0.
Gọi M là điểm biểu diễn của z.
Tìm được M ( -2; 2) nên z = -2+ 2i . Suy ra: