Cho cấp số cộng có u 1 = - 2 và d=3. Tính tổng của 25 số hạng đầu tiên của cấp số cộng.
A. 847
B. 850
C.853
D.856
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2023
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1 2022
\(\left\{{}\begin{matrix}u_1+d=3\\u_1+9d=-15\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=\dfrac{21}{4}\\d=-\dfrac{9}{4}\end{matrix}\right.\)
\(S_{20}=\dfrac{21}{4}.20+\dfrac{19.20}{2}.\left(-\dfrac{9}{4}\right)=-\dfrac{645}{2}\)
CM
23 tháng 5 2017
Đáp án B
Ta có: u 4 = u 1 + 3 d ⇒ u 1 = u 4 - 3 d = - 12 - 3 . 3 = - 21
Suy ra S 16 = 16 . u 1 + 16 . 15 2 d = 16 . - 21 + 16 . 15 2 . 3 = 24
CM
8 tháng 6 2019
Chọn D.
Phương pháp
Tổng của n số hạng đầu của CSC có số hạng đầu là u1 và công sai d:
CM
14 tháng 8 2017
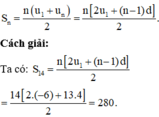
Chọn D
Phương pháp
Tổng của n số hạng đầu của CSC có số hạng đầu là u1 và công sai d:
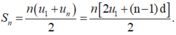
Cách giải:
Ta có: S 14 = n 2 u 1 + ( n - 1 ) d 2 = 280
CM
7 tháng 4 2019
Chọn C.
Đặt a = u1 thì u22 + u32 + u42 = (a + d)2 + (a + 2d)2 + (a + 3d2 = 3a2 – 36a + 126 = 3(a – 6)2 + 18 ≥ 18 với mọi a.
Dấu bằng xảy ra khi a – 6 = 0 hay a = 6.
Suy ra 6 = u1.
Ta có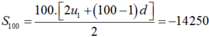 
CM
23 tháng 12 2019
Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
CM
14 tháng 1 2017
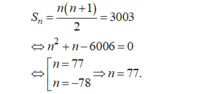
Chọn C.
Đặt a = u1 thì u22 – 2u32 – u42 = (a + d)2 – 2(a + 2d)2 – (a + 3d)2 = -2a2 – 12a – 12d2 = -2(a + 3)2 + 6 ≤ 6 với mọi a.
Dấu bằng xảy ra khi a + 3 = 0 hay a = -3.
Suy ra u1 = -3.
Ta có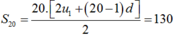 
.
CM
3 tháng 3 2018
Chọn C
Sử dụng tính chất của cấp số cộng và công thức tính tổng n số hạng đầu của cấp số cộng là
S n = n . u 1 + n ( n - 1 ) 2 . d
Đáp án B