Cho hình chóp S.ABCD, các cặp đường thẳng nào sau đây chéo nhau?
A. AB và CD
B. AD và BC
C. SA và BD
D. AC và BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) AB=CD; BC=AD.
b) Hai cặp cạnh AB và CD song song với nhau, BC và AD song song với nhau.
c) Sử dụng thước đo các cạnh ta thấy OA=OC; OB=OD.

Chọn C, bởi vì AC ko thể vuông góc với SB và SD được mà chỉ có thể vuông góc với BD thôi

Chọn đáp án B
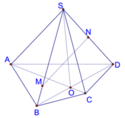
+ Giả sử SO, AD cắt nhau. Khi đó SO, AD đồng phẳng, suy ra S thuộc mp (ABCD) (Vô lý). Đáp án A bị loại.
+ Giả sử MN cắt SC. Khi đó MN và SC đồng phẳng, suy ra C thuộc (SBD) (Vô lý). Do đó đáp án C bị loại.
+ Giả sử SA cắt BC. Khi đó SA, BC đồng phẳng. Suy ra S thuộc mp (ABCD) (Vô lý). Đáp án D bị loại. MN, SO cùng nằm trong mp (SBD), không song song và trùng nhau.


Ta có S C D ∩ A B C D = C D
C D ⊥ S A C D ⊥ A C ⇒ C D ⊥ S A C ⇒ S C ⊥ C D
Vì S C ⊥ C D , S C ⊂ S C D A C ⊥ C D , A C ⊂ A B C D
Nên S C D , A B C D ^ = S C A ^ = 45 o
Dễ thấy ∆ S A C vuông cân tại A
Suy ra SA = AC = a 2
Lại có
S M C D = 1 2 M C . M D = 1 2 a . a = a 2 2
Do đó
V = V S . M C D = 1 3 S M C D S A = 1 3 . a 2 2 . a 2 = a 3 2 6
Ta có
B D ∥ M N M N ⊂ S M N ⇒ B D ∥ S M N
Khi đó d( SM,BD ) = d( SM, (SMN) ) = d( D, (SMN) ) = d( A, ( SMN) )
Kẻ A P ⊥ M N , P ∈ M N A H ⊥ S P , H ∈ S P
Suy ra A H ⊥ S M N ⇒ d A S M N = A H
∆ S A P vuông tại A có
1 A H 2 = 1 S A 2 + 1 A P 2 = 1 S A 2 + 1 A N 2 + 1 A M 2 = 1 2 a 2 + 1 a 2 4 + 1 a 2 = 11 2 a 2
Do đó d = d( SM, BD ) = AH = a 22 11
Đáp án A
SA chéo BD
Đáp án C