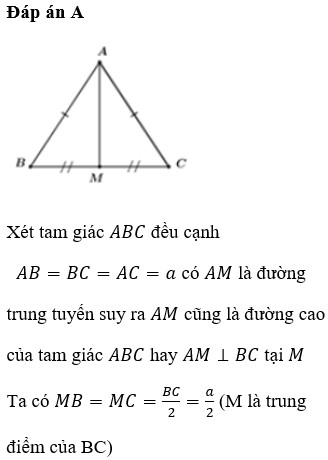
Đường cao của tam giác đều cạnh có bình phương độ dài là
A. 3 a 2 4
B. a 2 4
C. 3 a 2 2
D. 3 a 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
TN
2
AH
Akai Haruma
Giáo viên
5 tháng 1 2022
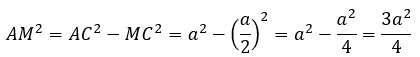
Lời giải:
Gọi đường cao tương ứng với cạnh huyền là $a$.
$S_{\triangle}=\frac{6.8}{2}=\frac{10a}{2}$
$\Rightarrow 6.8=10a4
$\Rightarrow a=4,8$
Đáp án C.
22 tháng 11 2016
Ta có:
\(S=pr=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\)
\(\Leftrightarrow p^2r^2=p\left(p-a\right)\left(p-b\right)\left(p-c\right)\)
\(\Leftrightarrow r^2=\frac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}\)
\(\Leftrightarrow\frac{1}{r^2}=\frac{p}{\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\frac{1}{\left(p-a\right)\left(p-b\right)}+\frac{1}{\left(p-b\right)\left(p-c\right)}+\frac{1}{\left(p-a\right)\left(p-c\right)}\)
\(\Leftrightarrow\frac{1}{r^2}=4\left(\frac{1}{\left(b+c-a\right)\left(a+c-b\right)}+\frac{1}{\left(a+c-b\right)\left(a+b-c\right)}+\frac{1}{\left(b+c-a\right)\left(a+b-c\right)}\right)\)
\(\Leftrightarrow\frac{1}{4r^2}=\frac{1}{c^2-\left(a-b\right)^2}+\frac{1}{a^2-\left(b-c\right)^2}+\frac{1}{b^2-\left(c-a\right)^2}\)
\(\ge\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)(áp dụng \(x^2-y^2\le x^2\))
\(\Rightarrow4r^2\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\le1\)
\(\Rightarrow\frac{1}{r^2\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)}\ge4\left(1\right)\)
Ta lại có
\(S=\frac{a.ha}{2}=pr=\frac{r\left(a+b+c\right)}{2}\)
\(\Rightarrow ha=\frac{r\left(a+b+c\right)}{a}\)
\(\Rightarrow ha^2=\frac{r^2\left(a+b+c\right)^2}{a^2}\)
Tương tự
\(hb^2=\frac{r^2\left(a+b+c\right)^2}{b^2}\)
\(hc^2=\frac{r^2\left(a+b+c\right)^2}{c^2}\)
Cộng vế theo vế ta được
\(ha^2+hb^2+hc^2=r^2\left(a+b+c\right)^2\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)
\(\Rightarrow\frac{\left(a+b+c\right)^2}{ha^2+hb^2+hc^2}=\frac{1}{r^2\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{\left(a+b+c\right)^2}{ha^2+hb^2+hc^2}\ge4\)
5 tháng 3 2016
a, Vì diện tích tam giác không đổi nên a.ha=b.hb=c.hc. Vì ha=hb=hc nên a=b=c
b, Dùng Pytago: Gọi x là độ dài các cạnh, M là trung điểm BC suy ra MB=x:2,
AB2+BM2AH2 suy ra x2+x2/4=a2.3/4 suy ra x=a