Biết rằng x, y là các số thực thỏa mãn điều kiện 1 < x < y . Tìm giá trị nhỏ nhất của biểu thức sau đây P = log x y - 1 2 + 8 log y x y x 2
A. 18
B. 9
C. 27
D. 30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\left(x+y\right)^3-3xy\left(x+y\right)+2x^2y^2\)
\(=2x^2y^2-3xy+1=2t^2-3t+\frac{5}{8}+\frac{3}{8}\) (đặt t = xy \(\Rightarrow t\le\frac{\left(x+y\right)^2}{4}=\frac{1}{4}\))
\(=\frac{1}{8}\left(4t-1\right)\left(4t-5\right)+\frac{3}{8}\ge\frac{3}{8}\)
Do đó \(P\ge\frac{3}{8}\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}x+y=1\\t=\frac{1}{4}\\x=y\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)
True?

\(x+y=1\Rightarrow x=1-y\)
\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)
\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)
=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)
Ta có :
\(x+y=1\Rightarrow\left(x+y\right)^2=1\)
\(\Leftrightarrow x^2+2xy+y^2=1\)
\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Hay \(C \ge \dfrac{3}{4}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

Từ đk trên ta có: \(2y^2+2zy+2z^2=2-3x^2\)
<=> \(3x^2+2y^2+2zy+2z^2=2\left(1\right)\)
<=>\(\left(x+y+z\right)^2+\left(x-y\right)^2+\left(x-z\right)^2=2\)
Do (x-y)2≥0; (x-z)2≥0 nên từ(*) suy ra (x+y+z)2≤2
Hay \(-\sqrt{2}\le x+y+z\le\sqrt{2}\)
Dấu "=" xảy ra khi x-y =0 và x-z=0 hay x=y=z
Thay vào (1) ta được 9x2=2 ; x=\(\dfrac{\sqrt{2}}{3};\dfrac{-\sqrt{2}}{3}\)
Với x=y=z =x=\(\dfrac{\sqrt{2}}{3};\dfrac{-\sqrt{2}}{3}\)thì max=\(\sqrt{2}\), min =\(-\sqrt{2}\)

Đáp án B.
Từ giả thiết, suy ra
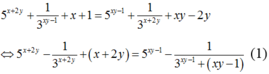
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 - ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f ( t ) luôn đồng biến trên ℝ .
Suy ra
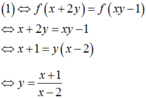
Do y > 0 nên x + 1 x - 2 > 0 ⇔ [ x > 2 x < - 1 . Mà x > 0 nên x > 2 .
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm
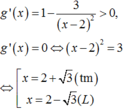
Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy min g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và x = 1 + 3 .
Đáp án C
Đặt t = y x > 1 ⇒ y = t x ⇒ P = log x t x 2 - 1 2 + 8 log t t x x 2
= log x t 2 + 1 2 + 8 log t t x - log t x 2 = 2 log x t 2 + 1 2 + 8 1 + log t x - 1 2 log t x 2
Đặt u = log t x ⇒ P = 2 u + 1 2 + 8 1 + 1 2 u 2 = 4 u 2 + 4 u + 2 u 2 + 8 u + 9 = P u
Do u = log x y x = log x y - 1 > 0 nên xét P u u > 0 ⇒ P ' u = 8 u + 4 - 4 u 3 - 8 u 2
= 4 2 u + 1 u 3 - 1 u 3 = 0 → u > 0 u = 1 . Do đó ta tìm được P m i n = P 1 = 27 .