Hai số phức z và - 1 z có điểm biểu diễn trong mặt phẳng phức là A, B. Khi đó
A. ∆ O A B vuông tại O
B. O, A, B thẳng
C. ∆ O A B đều
D. ∆ O A B cân tại O
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(z=a+bi\Rightarrow\overline{z}=a-bi\)
Ta có \(z.\overline{z}=1\Leftrightarrow\left(a+bi\right)\left(a-bi\right)=1\)
\(\Leftrightarrow a^2-b^2i^2=1\Leftrightarrow a^2+b^2=1\)
\(\Rightarrow\) Tập hợp các số phức thỏa mãn điều kiện trên là một đường tròn có tâm là gốc tọa độ, bán kính 1 đơn vị độ dài

Đáp án A.
Chọn z 1 = 1 ⇒ z 2 = 1 ± i 3 2 ⇒ z 2 − z 1 = − 1 ± i 3 2 .

Đáp án A.
Cách 1: Ta có:
![]()
![]()
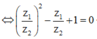
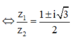
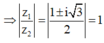
![]()
mặt khác 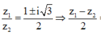
![]()
Do đó tam giác OAB là tam giác đều.
Cách 2: Chọn 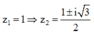
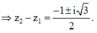
Ta có O A = ( x;y )
- 1 z = - 1 x - y i = - x - y i x 2 + y 2 = - x x 2 + y 2 - y x 2 + y 2 i ⇒ O B = - x x 2 + y 2 ; - y x 2 + y 2
Rõ ràng O A và O B cùng phương nên ba điểm O, A, B thẳng hàng
Đáp án B