Cho tam giác ABCABC, các đường cao BDBD và CECE. Chứng minh rằng:
a) Bốn điểm B, E, D, CB, E, D, C cùng thuộc một đường tròn.
b) DE<BC
giải giúp mình với.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2021
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
28 tháng 2 2023
a: Xét tứ giác CDHF có
góc CDF=góc CHF=90 độ
=>CDHF là tứ giác nội tiếp
b: Xét ΔBCA vuông tại C và ΔCDE vuông tại D có
góc CBA=góc DCE
=>ΔBCA đồng dạng với ΔCDE
=>DE/CA=CE/AB
=>DE*AB=CE*CA
BD là phân giác
=>DA/DC=BA/BC
mà CE/CD=BA/BC
nên DA=CE
=>DE*AB=AC*DA
5 tháng 12 2023
a: Xét tứ giác ADBE có
\(\widehat{ADB}+\widehat{AEB}=90^0+90^0=180^0\)
nên ADBE là tứ giác nội tiếp
=>A,D,B,E cùng thuộc một đường tròn
b: Xét tứ giác ADCF có
\(\widehat{ADC}+\widehat{AFC}=90^0+90^0=180^0\)
nên ADCF là tứ giác nội tiếp
=>A,D,C,F cùng thuộc một đường tròn
c: Xét tứ giác BEFC có
\(\widehat{BEC}=\widehat{BFC}=90^0\)
=>BEFC là tứ giác nội tiếp
=>B,E,F,C cùng thuộc một đường tròn
CM
18 tháng 12 2019
a) Gọi M là trung điểm của BC.
=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.
20 tháng 9 2021
a: Xét tứ giác ABDE có
\(\widehat{ADB}=\widehat{AEB}\left(=90^0\right)\)
Do đó: ABDE là tứ giác nội tiếp
hay A,B,D,E cùng thuộc một đường tròn
LS
25 tháng 4 2017
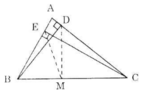
a) Gọi O là trung điểm của BC.
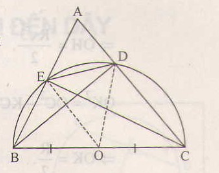
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
EO=12BC;DO=12BC.EO=12BC;DO=12BC.
Suy ra OE=OD=OB=OC(=12BC)OE=OD=OB=OC(=12BC)
Do đó 4 điểm B, C, D, E cùng thuộc đường tròn (O) đường kính BC.
b) Xét đường tròn nói ở câu a), BC là đường kính, DE là một dây không qua tâm, do đó DE<BC.
H9
HT.Phong (9A5)
CTVHS
19 tháng 6 2023
a) Gọi O là trung điểm của BC
Theo tính chất trung tuyến ứng với cạnh huyền ta có:
\(ED=\dfrac{1}{2}BC,DO=\dfrac{1}{2}BC\)
\(\Rightarrow OE=OD=OB=OC\left(=\dfrac{1}{2}BC\right)\)
Do đó 4 điểm B, E, C, D cùng thuộc đường tròn O đường kính BC
b) Xét đường \(\left(O;\dfrac{BC}{2}\right)\), BC là đường kính và DE là dây không qua tâm nên:
\(DE< BC\)
GH
19 tháng 6 2023
a.
Vì 2 tam giác vuông BEC và BDC có chung cạnh huyền BC nên 2 đỉnh góc vuông D và E nằm trên đường tròn đường kính BC.
Vậy 4 điểm B, E, D, C cùng thuộc 1 đường tròn.
b.
Trong đường tròn đường kính BC, DE là một dây không đi qua tâm. Vậy DE < BC (tính chất độ dài đường kính và dây cung)
24 tháng 7 2021
1) Xét tứ giác BCDE có
\(\widehat{BEC}=\widehat{BDC}\left(=90^0\right)\)
nên BCDE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
hay B,C,D,E cùng thuộc 1 đường tròn(đpcm)
CM
7 tháng 8 2019
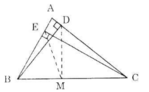
Gọi M là trung điểm của BC.
=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
HH
20 tháng 1 2021
a) Gọi O là trung điểm của BC ( OB = OC )
+) Xét tam giác vuông EBC ( ^BEC = 90^o )
EO là đường trung tuyến
\(\Rightarrow EO=\frac{1}{2}BC\)
\(\Rightarrow OE=OB=OC\left(1\right)\)
+) Xét tam giác vuông DBC ( ^CDB = 90^o )
DO là đường trung tuyến \(\Rightarrow DO=\frac{1}{2}BC\)
=> DO = OB = OC (2)
Từ (1)(2) => OD = OE = OB = OC
Vậy : 4 điểm B , E , D , C cùng thuộc đường tròn đường trình BC ( đpcm )
a: Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp