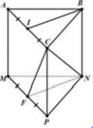
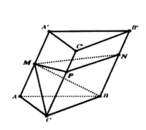
Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi
G
1
;
G
2
;
G
3
;
G
4
lần lượt là trọng tâm của các tam giác ABC, ACM, AMB, BCM,
V
1
là thể tích của khối tứ diện
G
1
G
2
G
3
G
4
...
Đọc tiếp
Cho lăng trụ tam giác ABC.MNP có thể tích V. Gọi lần lượt là trọng tâm của các tam giác ABC, ACM, AMB, BCM, là thể tích của khối tứ diện Khẳng định nào sau đây là đúng?
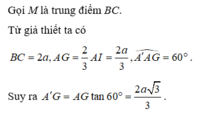
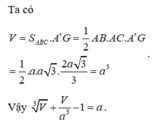
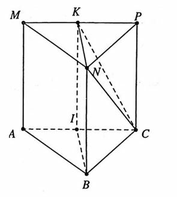
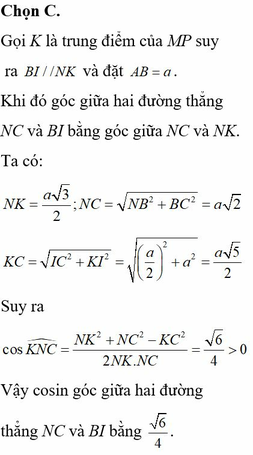
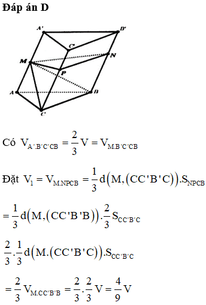
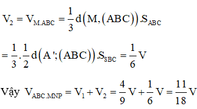
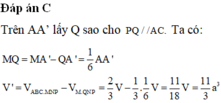
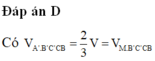
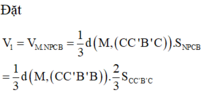
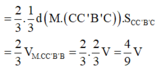
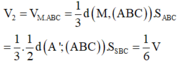
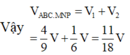
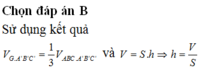
Đáp án C.
Phương pháp
So sánh diện tích đáy và chiều cao của các khối chóp.
Cách giải
Gọi D, E, F lần lượt là trung điểm của AC, AB, BC.
Vì G 2 ; G 3 ; G 4 là trọng tâm các tam giác MAC, MAB, MBC nên
G 2 ∈ M D ; M G 2 = 2 D G 2 G 3 ∈ M E ; M G 3 = 2 E G 3 G 4 ∈ M F ; M G 4 = 2 F G 4 ⇒ G 2 G 3 G 4 / / D E F ⇒ V 1 = V E . G 2 G 3 G 4 = F G 3 M G 3 . V M . G 2 G 3 G 4 = 1 2 V M . G 2 G 3 G 4
Lại có
V M . G 2 G 3 G 4 V M D E F = M G 2 . M G 3 . M G 4 M D . M E . M F = 2 3 . 2 3 . 2 3 = 8 27
⇒ V 1 = 1 2 8 27 V M D E F = 4 27 V M D E F
Lại có
S D E F = 1 4 S A B C ⇒ V M . D E F = 1 4 V M . A B C = 1 4 . 1 3 V = 1 12 V
Vậy
V 1 = 4 27 . V 12 = V 81