Cho hình chóp đều S.ABC có A B = a , A S B ^ = 30 0 . Lấy các điểm B',C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó
A. 3 - 1 a .
B. 3 a .
C. a 1 + 3 .
D. 1 + 3 a .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
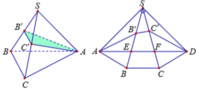
Trải tứ chóp S.ABC ra mặt phẳng (SBC) thì chu vi tam giác AB'C' bằng
![]()
Dấu “=” xảy ra khi ![]()
Ta có 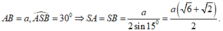
Lại có ![]()
Vậy chu vi tam giác AB'C' đạt giá trị nhỏ nhất bằng ![]()

Đáp án A
Ta có
S A ' S A = 2 5 ; S B ' S B = 1 4 ; S C ' S C = 1 3 . ⇒ V S A ' B ' C ' V S A B C = 2 5 . 1 4 . 1 3 = 1 30 .

Đáp án A.
Hướng dẫn giải:
Nếu a = b = c = 1 thì SA = SA',SB = SB',SC = SC'
nên ( A B C ) ≡ ( A ' B ' C ' )
Dễ thấy (A'B'C') đi qua trọng tâm của tam giác ABC
⇒ a + b + c = 3 là đáp án đúng