Cho dãy số xác định bởi Khi đó bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương pháp: Tìm công thức số hạng tổng quát
Cách giải: Ta có:
u ( 1 ) = 1
u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1
u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2
u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3
. . .
u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016
⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:
u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15
Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:
n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10
Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.
a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5
Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.
b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:
(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1
Vậy số hạng thứ mấy có giá trị 137137 là u1.

2:
a: \(u_1=\dfrac{2-1}{1+1}=\dfrac{1}{2}\)
\(u_2=\dfrac{2\cdot2-1}{2+1}=1\)
\(u_3=\dfrac{2\cdot3-1}{3+1}=\dfrac{5}{4}\)
\(u_4=\dfrac{2\cdot4-1}{4+1}=\dfrac{7}{5}\)
b: Đặt \(\dfrac{2n-1}{n+1}=\dfrac{13}{7}\)
=>7(2n-1)=13(n+1)
=>14n-7=13n+13
=>n=20
=>13/7 là số hạng thứ 20 trong dãy
1:
a: u1=1^2-1=0
u2=2^2-1=3
u3=3^2-1=8
u4=4^2-1=15
b: 99=n^2-1
=>n^2=100
mà n>=0
nên n=10
=>99 là số thứ 10 trong dãy

1:
a:
u1=1^2+1=2
u2=2^2+1=5
u3=3^2+1=10
u4=4^2+1=17
b: Đặt 101=n^2+1
=>n^2=100
=>n=10
=>101 là số hạng thứ 10
2:
a: \(u1=\dfrac{1+1}{2-1}=2\)
\(u2=\dfrac{2+1}{2\cdot2-1}=\dfrac{3}{3}=1\)
\(u_3=\dfrac{3+1}{2\cdot3-1}=\dfrac{4}{5}\)
\(u_4=\dfrac{4+1}{2\cdot4-1}=\dfrac{5}{7}\)
b: Đặt \(\dfrac{n+1}{2n-1}=\dfrac{31}{59}\)
=>59(n+1)=31(2n-1)
=>62n-31=59n+59
=>3n=90
=>n=30
=>31/59 là số hạng thứ 30 trong dãy

Chọn A.
Chúng ta đi tìm công thức xác định số hạng tổng quát của dãy số (an).
Đặt bn = an + 5 khi đó bn+1 = an+1 + 5.
Từ hệ thức truy hồi an+1 = 3an + 10 suy ra bn+1 – 5 = 3(bn – 5) + 10 ⇔ bn+1 = 3bn.
Như vậy ta có b1 = a1 + 5 = 6; bn+1 = 3bn.
Ta có b2 = 3b1; b3 = 3b2 = 32b1; b4 = 3b3 = 33b1.
Bằng phương pháp quy nạp ta chứng minh được rằng bn = 3n-1b1, ∀ n ∈ R*, suy ra an = 2.3n – 5, ∀ n ∈ R*.
Do đó a15 = 28697809.

Chọn D.
Ta có 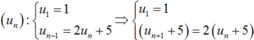
Đặt: vn = un + 5 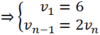
Khi đó ta được dãy mới; là cấp số nhân với : v1 = 6; q = 2
⇒ v2018 = 22017.v1 = 6.22017 ⇒ u2018 = 6.22017 – 5.
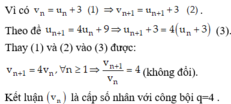


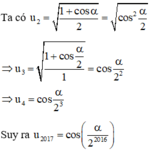
Đáp án A.
Ta có
n − 1 n 2 + 3 n + 2 = n − 1 n + 1 n + 2 = A n + 1 + B n + 2 ⇒ A + B = 1 2 A + B = − 1 ⇔ A = − 2 B = 3 .
Lại có 3 u n + 1 = 2 u n − 2 n + 1 + 3 n + 2
⇔ 3 u n + 1 − 1 n + 2 = 2 u n − 1 n + 1 .
Đặt v n = u n − 1 n + 1 ⇒ v 1 = 1 2
và v n = u n − 1 n + 1 → v n
là cấp số nhân với v 1 = 1 2 ; q = 1 3
⇒ v n = 1 2 . 2 3 n − 1 = 3 4 . 2 3 n → u n = v n + 1 n + 1 = 3 4 . 2 3 n + 1 n + 1 = 2 n − 2 3 n − 1 + 1 n + 1 .
⇒ u 2018 = 2 n − 2 3 n − 1 + 1 n + 1 n = 2018 = 2 2016 3 2017 + 1 2019 .