Cho hình lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a. Mặt phẳng đi qua A'B' và trọng tâm tam giác ABC cắt AC và BC lần lượt tại E và F. Tính thể tích V của khối chóp C.A'B'FE. A.
V
=
5
a
3
3
54
B.
V
=
5
a
3
3
18
C.
V
=
2
a
3
3
27
D.
V
=
2
a
3
...
Đọc tiếp
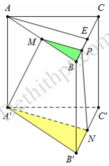
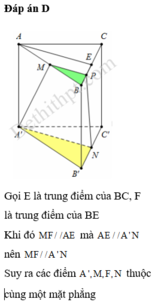
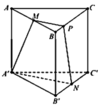
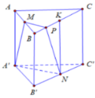
Cho hình lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a. Mặt phẳng đi qua A'B' và trọng tâm tam giác ABC cắt AC và BC lần lượt tại E và F. Tính thể tích V của khối chóp C.A'B'FE.
A. V = 5 a 3 3 54
B. V = 5 a 3 3 18
C. V = 2 a 3 3 27
D. V = 2 a 3 3 9
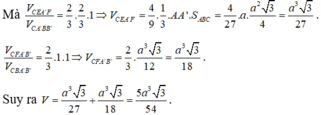
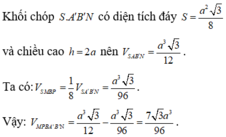
Đáp án A
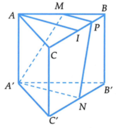
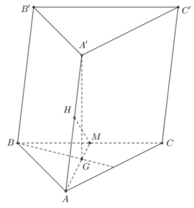
Gọi K là trọng tâm tam giác ABC. Qua K kẻ đường thẳng song song với A'B' lần lượt cắt AC; BC tại E và F. Gọi I là giao của CK và AB. Ta có
C I ⊥ A B B ' A ' ⇒ V C B A ' B ' = 1 3 . C I . S B A ' B ' = 1 3 . a 3 2 . a 2 2 = a 3 13 12 .
Kí hiệu như hình vẽ. Ta có V = V C F A ' B ' + V C E A ' F .
Mà V C E A ' F C A ' B B ' = 2 3 . 2 3 . 1 ⇒ V C E A ' F = 4 9 . 1 3 . A A ' . S A B C = 4 27 . a . a 2 3 4 = a 3 3 27 .
V C F A ' B ' C B A ' B ' = 2 3 . 1 . 1 ⇒ V C F A ' B ' = 2 3 . a 3 3 12 = a 3 13 18 . Suy ra V = a 3 3 27 + a 3 3 18 = 5 a 3 3 54 .