H Cho hình lập phương . Gọi H ' là hình bát diện đều có các đỉnh là tâm các mặt của H . Tính tỉ số thể tích của H ' và H .
A. 1 2
B. 1 4
C. 1 6
D. 1 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 3 2018
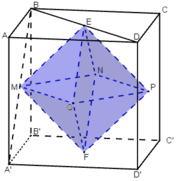
Gọi a là cạnh của hình lập phương ABCD. A 1 B 1 C 1 D 1 ;
⇒ Diện tích toàn phần của hình lập phương (H) là: SH = 6.a2 (đvdt).
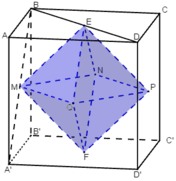
Gọi tâm các mặt lần lượt là E, F, M, N, P, Q như hình vẽ.
⇒ (H’) là bát diện đều EMNPQF.
+ Áp dụng định lí pytago vào tam giác vuông AA’D ⇒ A’D = a√2
+ EM là đường trung bình của ΔBA’D
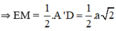
⇒ (H’) là bát diện đều gồm 8 mặt là các tam giác đều cạnh bằng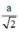 
⇒ Diện tích một mặt của (H’) là:
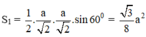
⇒ Diện tích toàn phần của (H’) là:
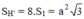
Vậy tỉ số diện tích cần tính là:
CM
27 tháng 11 2017
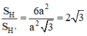
Gọi a là cạnh của hình lập phương ABCD.A1B1C1D1;
⇒ Diện tích toàn phần của hình lập phương (H) là: SH = 6.a2 (đvdt).
Gọi tâm các mặt lần lượt là E, F, M, N, P, Q như hình vẽ.
⇒ (H’) là bát diện đều EMNPQF.
+ Áp dụng định lí pytago vào tam giác vuông AA’D ⇒ A’D = a√2
+ EM là đường trung bình của ΔBA’D
QUẢNG CÁO
⇒ (H’) là bát diện đều gồm 8 mặt là các tam giác đều cạnh bằng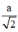 
⇒ Diện tích một mặt của (H’) là:
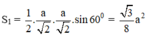
⇒ Diện tích toàn phần của (H’) là:
Vậy tỉ số diện tích cần tính là:
1 tháng 4 2017
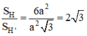
Cho hình lập phương ABCD.A’B’C’D’ . Gọi E, F, G, I, J, K là tâm của các mặt của nó. Khi đó các đỉnh E, F, G, I, J, K tạo thành hình bát diện đều EFGIJK.
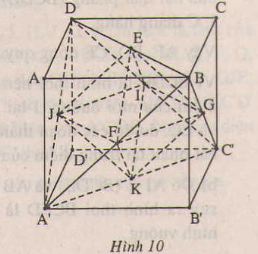
Đặt AB = a, thì 
Diện tích tam giác đều (EFJ) bằng .gif)
.
Suy ra diện tích toàn phần của hình bát diện (H’) bằng .gif)
. Diện tích toàn phần của hình lập phương (H) bằng .gif)
. Do đó tỉ số diện tích toàn phần của (H) và (H') bằng
.gif)
.
CM
29 tháng 1 2019
Đáp án C.
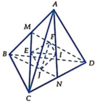
Đặt (H) là hình tứ diện đều ABCD, cạnh bằng A. Gọi E ; F ; I ; J lần lượt là tâm của các mặt A B C ; A B D ; A C D ; B C D .
Kí hiệu như hình vẽ.
Ta có M E M C = M F M D = 1 3 ⇒ E F C D = 1 3 ⇒ E F = C D 3 = a 3 .
Vậy tứ diện là tứ diện đều có cạnh bằng a 3 .
Tỉ số thể tích của diện tích toàn phần tứ diện đều và tứ diện đều ABCD là a 3 a 2 = 1 9
CM
6 tháng 7 2017
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là a/2. Khi đó
Từ đó suy ra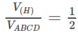 
20 tháng 5 2017
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \(\dfrac{a}{2}\). Khi đó :
\(V_{ABCD}=a^3\dfrac{\sqrt{2}}{12};V_{\left(H\right)}=\dfrac{1}{3}\left(\dfrac{a}{2}\right)^3\sqrt{2}=a^3\dfrac{\sqrt{2}}{24}\)
Từ đó suy ra :
\(\dfrac{V_{\left(H\right)}}{V_{ }ABCD}=\dfrac{1}{2}\)
CM
12 tháng 4 2017
Đáp án D
Gọi M = (D'E) ∩ (DA), N = (D'F) ∩ (DC). Dễ thấy MN đi qua B, các hình chóp E.AMB và F.CNB có diện tích đáy và chiều cao bằng nhau. Áp dụng công thức (7) ta có:
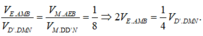
Áp dụng ví dụ 9, ta có:
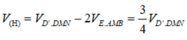
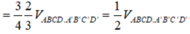
Suy ra V(H) = V(H'). Do đó k = 1.
Đáp án C.
Cho hình lập phương ABCD.A'B'C'D'. Gọi E,F,G,I,J,K là tâm các mặt của nó. Khi đó các đỉnh E,F,G,I,J,K tạo thành hình bát diện đều EFGHIJK.
Đặt A B = a thì E J = A ' B 2 = a 2 2 .
Thể tích của khối bát diện đều có cạnh bằng x được tính bằng công thức V = x 3 2 3 . Áp dụng vào bài toán ta có V E F G Ị K = 1 3 . a 2 2 3 . 2 = a 3 6 .
Vậy tỉ số thể tích cần tìm là a 3 6 a 3 = 1 6 .