Gọi x 1 , x 2 là hai điểm cực trị của hàm số y = 1 3 x 3 − 1 2 m x 2 − 4 x − 10 . Tìm giá trị lớn nhất của biểu thức S = x 1 2 − 1 x 2 2 − 1 .
A. 9
B. 4
C. 0
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
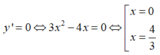
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.

\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).

TXĐ: D = R
\(y'=3x^2-6x=0\) \(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=1\\x=2\Rightarrow y=-3\end{matrix}\right.\)
Suy ra 2 điểm cực trị của đồ thị là: A(0; 1) và B(2; -3)
Ptđt đi qua 2 điểm cực trị:
\(\dfrac{x}{2}=\dfrac{y-1}{-4}\) \(\Rightarrow-2x=y-1\) \(\Leftrightarrow y=-2x+1\left(d'\right)\)
Vì \(d\perp d'\) \(\Rightarrow\left(2m-1\right)\cdot\left(-2\right)=-1\) \(\Leftrightarrow m=\dfrac{3}{4}\)
Chọn B
Phương pháp:
+) Xác định giá trị của m để hàm số đã cho có cực trị.
+) Sử dụng hệ thức Vi-ét để tìm giá trị lớn nhất của biểu thức S.
Cách giải: