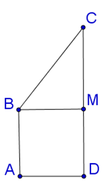
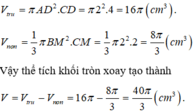Cho một hình vuông ABCD cạnh a. Khi quay hình vuông theo trục chéo AC thì ta thu được một khối tròn xoay có thể tích V 1 và quay quan trục AB được khối tròn xoay có thể tích V 2 . Khi đó V 1 V 2 bằng
A. 2 2
B. 2 3
C. 2 6
D. π 2 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi O là tâm hình vuông ABCD
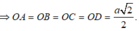
⇒ V 1 = 2 . 1 3 . O A . S ( O ; O B ) = a 2 3 π 6 (đvtt)
V 2 = A B . S ( O ; A D ) = A B . π . AD 2 = a 3 π
⇒ V 1 V 2 = 2 6

Đáp án D
Khi quay hình thang cân ABCD quanh trục đối xứng ta được hình nón cụt có chiều cao h = 2 a 2 và bán kính 2 đáy là R 1 = a , R 2 = 2 a .
Vậy thể tích cần tính là V = πh 3 R 1 2 + R 2 2 + R 1 R 2 = 14 2 3 πa 3

Đáp án C.
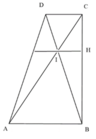
Phần thể tích chung của 2 hình nón T1 và T2 là 2 hính nón tạo bởi việc quay 2 tam giác HIB và HIC quanh BC.
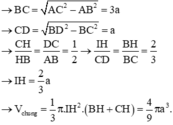

Đáp án A
Ta có thể tích khối tròn xoay tạo thành bằng hiệu thể tích hình trụ bán kính đáy AD, chiều cao CD trừ cho thể tích nón đỉnh B, bán kính đáy BM chiều cao CM.
Ta có