Cho hàm số y = x 3 + 3 m x 2 − m có đồ thị (C). Tất cả các giá trị của tham số thực m để (C) có hai điểm cực trị nằm về cùng một phía so với trục hoành là
A. m < − 1 2 h o ặ c m > 1 2
B. − 1 2 < m < 1 2 v à m ≠ 0
C. 0 < m < 1 2
D. − 1 2 < m ≤ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đạo hàm y’ = 3x2+6x+m. Ta có ∆ ' y ' = 9 - 3 m
Hàm số có cực đại và cực tiểu khi ∆ ' y ' = 9 - 3 m > 0 ⇔ m < 3
Ta có 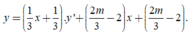
Gọi x1; x2 là hoành độ của hai điểm cực trị khi đó
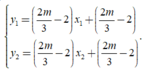
Theo định lí Viet, ta có 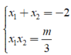
Hai điểm cực trị nằm về hai phía trục hoành khi y1.y2<0
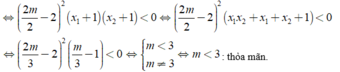
Chọn C.

Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
![]()
![]()
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
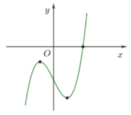
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.

Đáp án C
TXĐ: D = ℝ .
Ta có y ' = x 2 − 2 m − 1 x + m − 1 .
Để đồ thị hàm số có hai điểm cực trị nằm về hai phía của trục tung thì
m − 1 2 − m − 1 > 0 m − 1 > 0 2 m − 1 > 0 ⇔ m > 2.
Vậy m>2 thỏa mãn điều kiện đề bài.
Đáp án B