Tính đạo hàm cấp 2 của hàm số y = 10 x
A. y ' ' = 10 x
B. y ' ' = 10 x ln 10
C. y ' ' = 10 x ln 2 10
D. y ' ' = 10 x l n 2 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

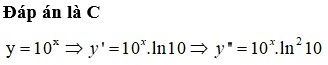

a: \(y'=4\cdot3x^2-3\cdot2x+2=12x^2-6x+2\)
b: \(y'=\dfrac{\left(x+1\right)'\left(x-1\right)-\left(x+1\right)\left(x-1\right)'}{\left(x-1\right)^2}=\dfrac{x-1-x-1}{\left(x-1\right)^2}=\dfrac{-2}{\left(x-1\right)^2}\)
c: \(y'=-2\cdot\left(\sqrt{x}\cdot x\right)'\)
\(=-2\cdot\left(\dfrac{x+x}{2\sqrt{x}}\right)=-2\cdot\dfrac{2x}{2\sqrt{x}}=-2\sqrt{x}\)
d: \(y'=\left(3sinx+4cosx-tanx\right)\)'
\(=3cosx-4sinx+\dfrac{1}{cos^2x}\)
e: \(y'=\left(4^x+2e^x\right)'\)
\(=4^x\cdot ln4+2\cdot e^x\)
f: \(y'=\left(x\cdot lnx\right)'=lnx+1\)

\(a,y'=\left[\left(2x-3\right)^{10}\right]'\\ =10\left(2x-3\right)^9\left(2x-3\right)'\\ =20\left(2x-3\right)^9\\ b,y'=\left(\sqrt{1-x^2}\right)'\\ =\dfrac{\left(1-x^2\right)'}{2\sqrt{1-x^2}}\\ =-\dfrac{2x}{2\sqrt{1-x^2}}\\ =-\dfrac{x}{\sqrt{1-x^2}}\)

\(a,y'=8x^3-9x^2+10x\\ \Rightarrow y''=24x^2-18x+10\\ b,y'=\dfrac{2}{\left(3-x\right)^2}\\ \Rightarrow y''=\dfrac{4}{\left(3-x\right)^3}\)
\(c,y'=2cos2xcosx-sin2xsinx\\ \Rightarrow y''=-5sin\left(2x\right)cos\left(x\right)-4cos\left(2x\right)sin\left(x\right)\\ d,y'=-2e^{-2x+3}\\ \Rightarrow y''=4e^{-2x+3}\)

\(y'=\dfrac{1}{4}\left(x^2-4x+10\right)^{-\dfrac{3}{4}}\left(x^2-4x+10\right)'\)
\(=\dfrac{x-2}{2\sqrt[4]{\left(x^2-4x+10\right)^3}}\)

a: y=ln(x+1)
=>\(y'=\dfrac{1}{x+1}\)
=>\(y''=\dfrac{1'\left(x+1\right)-1\left(x+1\right)'}{\left(x+1\right)^2}=\dfrac{-1}{\left(x+1\right)^2}\)
b: y=tan 2x
=>\(y'=\dfrac{2}{cos^22x}\)
=>\(y''=\left(\dfrac{2}{cos^22x}\right)'=\dfrac{-2\cdot cos^22x'}{cos^42x}=\dfrac{-2\cdot2\cdot cos2x\left(cos2x\right)'}{cos^42x}\)
\(=\dfrac{4\cdot2\cdot sin2x}{cos^32x}=\dfrac{8\cdot sin2x}{cos^32x}\)

Ta có:\(\left(x^{10}\right)'=10x^9\).
Từ đó:\(y'\left(-1\right)=10.\left(-1\right)^9=-10\) và \(y'\left(\sqrt[3]{2}\right)=10.\left(\sqrt[3]{2}\right)^9=80\).

a: \(y=x\cdot e^{2x}\)
=>\(y'=\left(x\cdot e^{2x}\right)'\)
\(=x\cdot\left(e^{2x}\right)'+x'\cdot\left(e^{2x}\right)\)
\(=e^{2x}+2\cdot x\cdot e^{2x}\)
\(y''=\left(e^{2x}+2\cdot x\cdot e^{2x}\right)'\)
\(=\left(e^{2x}\right)'+\left(2\cdot x\cdot e^{2x}\right)'\)
\(=4\cdot e^{2x}+4\cdot x\cdot e^{2x}\)
b: \(y=ln\left(2x+3\right)\)
=>\(y'=\dfrac{\left(2x+3\right)'}{\left(2x+3\right)}=\dfrac{2}{2x+3}\)
=>\(y''=\left(\dfrac{2}{2x+3}\right)'=\dfrac{2\left(2x+3\right)'-2'\left(2x+3\right)}{\left(2x+3\right)^2}\)
\(=\dfrac{4}{\left(2x+3\right)^2}\)