Cho hai số thực x, y thỏa mãn
0
≤
x
≤
1
2
,
0
<
y
≤
1
và
log
11
−
2
x
−
y
=
2
y
+
4
x
−
1.
Xét biểu thức
P
=
16
x
2
y
−
2
x
3
y
+
2
−
y
+
5.
Gọi m, M lần lượt là giá trị nhỏ nhất và...
Đọc tiếp
Cho hai số thực x, y thỏa mãn 0 ≤ x ≤ 1 2 , 0 < y ≤ 1 và log 11 − 2 x − y = 2 y + 4 x − 1. Xét biểu thức P = 16 x 2 y − 2 x 3 y + 2 − y + 5. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của P. Khi đó giá trị của biểu thức T = 4m + M bằng bao nhiêu?
A. 16
B. 18
C. 17
D. 19
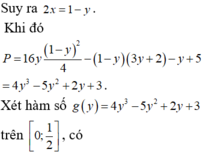
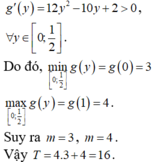
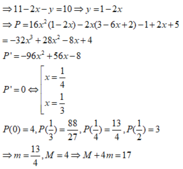
Đáp án C
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17