Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB= 3 , AD= 7 . Hai mặt bên (ABB'A'),(ADD'A') tạo với đáy các góc lần lượt là 45 ° và 60 ° . Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1.
A. V = 3
B. V = 7 3
C. V = 3
D. V = 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

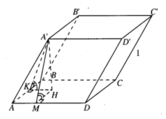
Gọi H là hình chiếu vuông góc của A' trên mặt phẳng (ABCD)
Kẻ HN vuông góc với AB tại N, HM vuông góc với AD tại M
Ta cần tìm chiều cao h=A'H của hình hộp
Dễ dàng chứng minh \(\widehat{A'NH}=60^0\) và \(\widehat{A'MH}=45^0\)
Xét tam giác vuông NHA' và MHB' có
\(NH=\frac{HA'}{tan\widehat{HNA'}}=\frac{h}{\sqrt{3}}\) và \(MH=\frac{HA'}{tan\widehat{HMA'}}=h\)
Xét hình vuông AMHN có \(AH=\sqrt{HN^2+HM^2}=\frac{2h}{\sqrt{3}}\)
Xét tam giác vuông AHA' có \(AH^2+A'H^2=A'A^2\Leftrightarrow h^2+\frac{4}{3}h^2=1\Leftrightarrow h=\sqrt{\frac{3}{7}}\)
Vậy thể tích hình hộp là: \(V=h.\sqrt{3}.\sqrt{7}=\sqrt{\frac{3}{7}}.\sqrt{3}\sqrt{7}=3\)

Đáp án A
![]()
![]()
Theo định lí 3 đường vuông góc, ta có
![]()
![]()
Ta cũng có HKAM là hình chữ nhật, đặt A'H = h ta có
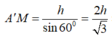
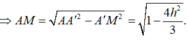
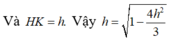
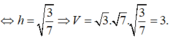

Chọn A
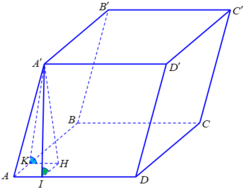
Gọi H là hình chiếu vuông góc của A' lên mặt phẳng (ABCD);

Theo giả thiết, ta có ![]()
=> ΔHKA' = ΔHIA' => HI = HK
=> tứ giác AIHK là hình vuông cạnh a, (a>0) => AH = a√2
Tam giác A'HK vuông cân tại H có HK=HA'=a
Tam giác AHA' vuông tại H có AA'²=AH²+A'H²
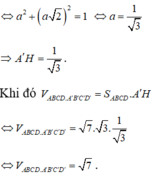

Đáp án B

A C = 2 S A = 2 tan 60 0 = 2 3 V = 1 3 .2 3 .1. 3 = 2