Question

[Thức Nguyễn Văn]

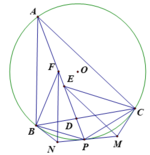
1. Cho ΔABC nội tiếp đường tròn (O). D, E, F lần lượt là trung điểm của BC, AC, AB. Kẻ DD' song song với OA, EE' song song với OB, FF' song song với OC. Chững minh DD', EE', FF' đồng quy

2. Cho tam giác ABC nội tiếp đường tròn (O;R). Diểm M thuộc cung nhỏ BC. Gọi I, K, H theo thứ tự là hình chiếu vuông góc của M trên AB, AC, BC. Gọi P, Q lần lượt là trung điểm của AB, HK

a) Chứng minh:ΔBMA đồng dạng ΔHMK

b) Chứng minh: ΔBMH đồng dạng ΔPMQ TỪ ĐÓ SUY RA MQ⊥PQ

c) Cho ΔABC đều. Xác định vị trí của điểm M trên cũng BC để MA+MB+MC đạt giá trị lớn nhất

3. Cho tam giác ABC nhọn và O là một điểm nằm trong tam giác. Các tia OA, BO, CO lần lược cắt BC, AC, AB tại M, N, P.

a) Chứng minh \(\frac{S_{BOC}}{S_{ABC}}=\frac{OM}{AM}\)

b) Chứng minh: \(\frac{AM}{OM}+\frac{BN}{ON}+\frac{CP}{OP}\)≥9