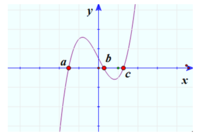
Cho hàm số y = a x 3 + b x 2 + c x + d a ≠ 0 có đồ thị (C). Biết rằng (C) cắt trục hoành tại ba điểm phân biệt có hoành độ x 1 > x 2 > x 3 > 0 và trung điểm của đoạn thẳng nối hai điểm cực trị của (C) có hoành độ x 0 = 1 3 . Biết rằng 3 x 1 + 4 x 2 + 5 x 3 2 = 44 x 1 x 2 + x 2 x 3 + x 3 x 1 . Tính tổng S = x 1 + x 2 2 + x 3 2
A. S = 137 216
B. S = 45 157
C. S = 133 216
D. S = 1





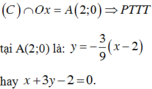
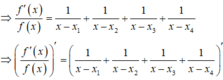
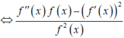
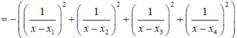
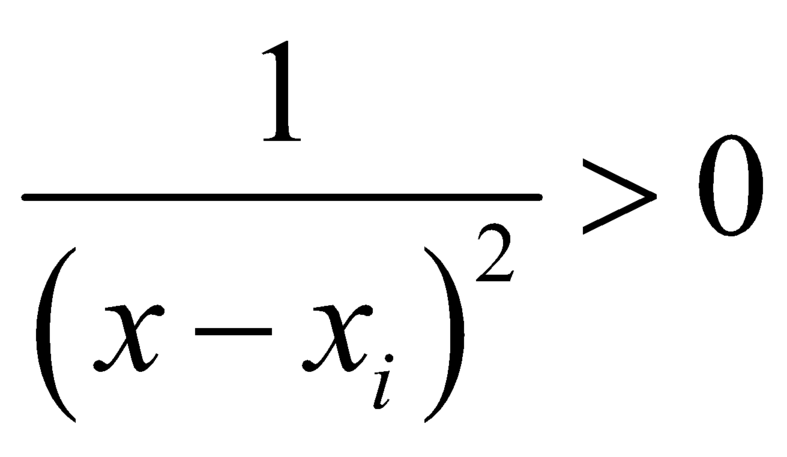 ,
, 
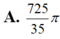
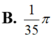

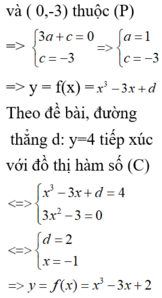
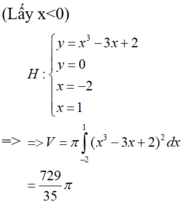
 Tính diện tích S của hình phẳng giới hạn bởi đồ thị
Tính diện tích S của hình phẳng giới hạn bởi đồ thị
Chọn đáp án C
Ta có
⇔ x = - b 3 a
Đồ thị (C) có hai điểm cực trị thì trung điểm của đoạn thẳng nối hai điểm cực trị đó chính là điểm uốn U của đồ thị và hoành độ của điểm U là nghiệm của phương trình y'' = 0. Từ giả thiết ta có
Lại có phương trình hoành độ giao điểm a x 3 + b x 2 + c x + d = 0 có ba nghiệm dương phân biệt x 1 , x 2 , x 3 .
Theo định lý Vi-ét ta có
Từ giả thiết
Áp dụng bất đẳng thức Cau-chy cho các số dương ta có:
; dấu “=” xảy ra khi 2 x 1 = 3 x 2
; dấu “=” xảy ra khi 2 x 1 = 6 x 3
; dấu “=” xảy ra khi x 2 = 2 x 3
Cộng theo vế của ba bất đẳng thức trên ta đươc
Dấu “=” xảy ra khi
Vậy S = x 1 + x 2 2 + x 3 2 = 133 216