Thực hiện phép nhân 1 1 - x . 1 1 + x . 1 1 + x 2 . 1 1 + x 4 . 1 1 + x 8 . 1 1 + x 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

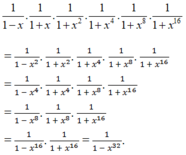

a: \(=\dfrac{5\left(x+2\right)}{10xy^2}\cdot\dfrac{12x}{x+2}=\dfrac{60x}{10xy^2}=\dfrac{6}{y^2}\)
b: \(=\dfrac{x-4}{3x-1}\cdot\dfrac{3\left(3x-1\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{3}{x+4}\)
c: \(=\dfrac{2\left(2x+1\right)}{\left(x+4\right)^2}\cdot\dfrac{\left(x+4\right)}{3\left(x+3\right)}=\dfrac{2\left(2x+1\right)}{3\left(x+3\right)\left(x+4\right)}\)
d: \(=\dfrac{5\left(x-1\right)}{3\left(x+1\right)}\cdot\dfrac{x+1}{x-1}=\dfrac{5}{3}\)

mình biết nội quy rồi nên đưng đăng nội quy
ai chơi bang bang 2 kết bạn với mình
mình có nick có 54k vàng đang góp mua pika
ai kết bạn mình cho
3(x - 1)(x - 2) - x(3x + 1)(1 - x)
=(3x - 3)(x - 2) - (3x^2 + x)(1 - x)
=3x^2 - 6x - 3x + 6 - (3x^2 - 3x^3 + 1 - x^2)
=3x^2 - 6x - 3x + 6 - 3x^2 +3x^3 - 1 + x^2
= -9x + 5 + x^2

Bài 1:
\(3a.\left(2a^2-ab\right)=6a^3-3a^2b\)
\(\left(4-7b^2\right).\left(2a+5b\right)=8a+20b-14ab^2-35b^3\)
Bài 2:
\(2x^2-6x+xy-3y=2x.\left(x-3\right)+y.\left(x-3\right)=\left(x-3\right).\left(2x+y\right)\)
Bài 3: Tại x = 3/2, y =1/3 thì Q = 67/9
Bài 4:
\(\left(\frac{1}{x+1}+\frac{2x}{1-x^2}\right).\left(\frac{1}{x-1}\right)\) \(\frac{1}{\left(x+1\right).\left(x-1\right)}+\frac{2x}{\left(1-x^2\right).\left(x-1\right)}=\frac{x-1}{\left(x+1\right).\left(x-1\right)^2}+\frac{-2x}{\left(x-1\right)^2.\left(x+1\right)}\)
= \(\frac{x-1-2x}{\left(x+1\right).\left(x-1\right)^2}=\frac{-\left(x+1\right)}{\left(x+1\right).\left(x-1\right)^2}=\frac{-1}{\left(x-1\right)^2}\)

\(\dfrac{1}{1-x}\cdot\dfrac{1}{1+x}\cdot\dfrac{1}{1+x^2}\cdot\dfrac{1}{1+x^4}\cdot\dfrac{1}{1+x^8}\cdot\dfrac{1}{1+x^{16}}\)
\(=\dfrac{1}{\left(1-x\right)\left(1+x\right)\left(1+x^2\right)\left(1+x^4\right)\left(1+x^8\right)\left(1+x^{16}\right)}\)
\(=\dfrac{1}{\left(1-x^2\right)\left(1+x^2\right)\left(1+x^4\right)\left(1+x^8\right)\left(1+x^{16}\right)}\)
\(=\dfrac{1}{\left(1-x^4\right)\left(1+x^4\right)\left(1+x^8\right)\left(1+x^{16}\right)}\)
\(=\dfrac{1}{\left(1-x^8\right)\left(1+x^8\right)\left(1+x^{16}\right)}\)
\(=\dfrac{1}{\left(1-x^{16}\right)\left(1+x^{16}\right)}\)
\(=\dfrac{1}{1-x^{32}}\)

a) \(\left(x+3\right)^2=\left(x+3\right)\left(x+3\right)\)
\(\Leftrightarrow\left(x+3\right)^2=\left(x+3\right)^2\)
\(\Leftrightarrow\left(x+3\right)^2-\left(x+3\right)^2=0\)
\(\Leftrightarrow0x=0\)( luôn đúng với mọi x )
Vậy tập nghiệm của phương trình là: \(S=\left\{x\inℝ\right\}\)
b) \(\left(x-1\right)^3=\left(x-1\right)\left(x-1\right)\left(x-1\right)\)
\(\Leftrightarrow\left(x-1\right)^3=\left(x-1\right)^3\)
\(\Leftrightarrow\left(x-1\right)^3-\left(x-1\right)^3=0\)
\(\Leftrightarrow0x=0\)( luôn đúng với mọi x )
Vậy tập nghiệm của phương trình là: \(S=\left\{x\inℝ\right\}\)

\(a,=12x^2-4x-6x-2-x-3=12x^2-11x-5\\ b,=12x^2-9x-12x^2-4x+5=5-13x\\ c,=12x^3-4x^2-12x^3-12x^2+7x-3=-16x^2+7x-3\\ d,=\left(x^2-4\right)\left(x^2+4\right)=x^4-16\)

\(=\dfrac{1+x+1-x}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{2+2x^2+2-2x^2}{1-x^4}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{4}{1-x^4}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+...+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{4+4x^4+4-4x^4}{1-x^8}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{8+8x^8+8-8x^8}{1-x^{16}}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{16+16x^{16}+16-16x^{16}}{1-x^{32}}=\dfrac{32}{1-x^{32}}\)

