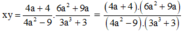Tính tích x.y, biết rằng x và y thỏa mãn các đẳng thức sau (a, b là các hằng số): 4 a 2 - 9 x = 4 a + 4 ; với a ≠ ± 3/2 và 3 a 3 + 3 y = 6 a 2 + 9 a với a ≠ - 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 10 2018
Vì a
≠
b nên
2
a
3
-
2
b
3
≠
0. Suy ra: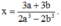 
Vì a
≠
- b nên a + b
≠
0. Suy ra: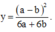 
Vậy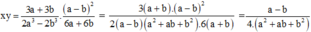 
18 tháng 8 2017
Ta có:
\(\frac{x^4}{a}+\frac{y^4}{b}\ge\frac{\left(x^2+y^2\right)^2}{a+b}=\frac{1}{a+b}\)
Dấu = xảy ra khi .... Làm tiếp nhé
18 tháng 8 2017
ta có: \(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\)=> \(\frac{bx^4+ay^4}{ab}=\frac{\left(x^2+y^2\right)^2}{a+b}\) (vì x^2 +y^2 =1)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(ab\left(x^4+2x^2y^2+y^4\right)\)
=>\(abx^4+b^2x^4+aby^4+a^2y^4\) = \(abx^4+2abx^2y^2+aby^4\)
=> \(b^2x^4-2abx^2y^2+a^2y^4=0\)
=>\(\left(bx^2-ay^2\right)^2=0\)=>\(bx^2=ay^2\Rightarrow\frac{x^2}{a}=\frac{y^2}{b}=\frac{x^2+y^2}{a+b}=\frac{1}{a+b}\)
=> \(\frac{x^{2012}}{a^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\) và \(\frac{y^{2012}}{b^{1006}}=\frac{1}{\left(a+b\right)^{1006}}\)
=>\(\frac{x^{2012}}{a^{1006}}+\frac{y^{2012}}{b^{1006}}=\frac{2}{\left(a+b\right)^{1006}}\)
22 tháng 8 2021
Bài 2:
a: Ta có: \(2x^2+y^2-2xy+x+2=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{7}{4}=0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}=0\left(vôlý\right)\)
b: Ta có: \(-x^2-26y^2+10xy-20y-150=0\)
\(\Leftrightarrow x^2-10xy+25y^2+y^2+20y+100+50=0\)
\(\Leftrightarrow\left(x-5y\right)^2+\left(y+10\right)^2+50=0\left(vôlý\right)\)
22 tháng 8 2021
Bài 1:
\(a+b+c=0\Leftrightarrow\left(a+b+c\right)^2=0\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\Leftrightarrow2\left(ab+bc+ca\right)=0-1=-1\)hay \(ab+bc+ca=-\dfrac{1}{2}\Leftrightarrow\left(ab+bc+ca\right)^2=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2a^2bc+2ab^2c+2abc^2=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2+2abc\left(a+b+c\right)=\dfrac{1}{4}\Leftrightarrow a^2b^2+b^2c^2+c^2a^2=\dfrac{1}{4}\)Ta có: \(P=a^4+b^4+c^4=\left(a^2+b^2+c^2\right)^2-2\left(a^2b^2+b^2c^2+c^2a^2\right)=1-2.\dfrac{1}{4}=\dfrac{1}{2}\)Vậy \(P=\dfrac{1}{2}\)
Vì a ≠ ± 3/2 nên 4 a 2 - 9 ≠ 0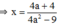
Vì a ≠ - 1 nên 3 a 3 + 3 ≠ 0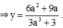
Do đó: