Cho các phương trình: x 2 + 2 x = 1 3
Hãy cộng vào hai vế của mỗi phương trình cùng một số thích hợp để được một phương trình mà vế trái thành một bình phương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 3 2018
Đúng(0)
Những câu hỏi liên quan
CM
19 tháng 11 2019
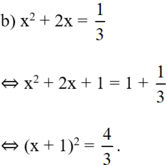
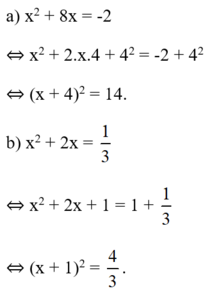
Kiến thức áp dụng
+ Các hằng đẳng thức:
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2.
4 tháng 4 2017
a) \(x^2+8x=-2\)
\(\Rightarrow x^2+2.x.4+16=-2+16\)
\(\Rightarrow\left(x+4\right)^2=14\)
b) \(x^2+2x=\dfrac{1}{3}\)
\(\Rightarrow x^2+2x+1=\dfrac{1}{3}+1\)
\(\Rightarrow\left(x+1\right)^2=\dfrac{4}{3}\)
CM
22 tháng 5 2018
Sử dụng tính chất “cộng hay trừ hai vế một bất đẳng thức với cùng một số và giữ nguyên chiều bất đẳng thức ta được một bất đẳng thức tương đương”.
Đáp án: A
CM
23 tháng 12 2019
Ta có : 3 x 2 – 6x + 5 = 0 ⇔ x 2 - 2x + 5/3 = 0
⇔ x 2 – 2x + 5/3 + 1 = 1 ⇔ x 2 – 2x + 1 = 1 - 5/3
⇔ x - 1 2 = -2/3
Ta thấy x - 1 2 ≥ 0 và -2/3 < 0
Vậy phương trình vô nghiệm.