Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn mốc thế năng tại mặt tấm đá.
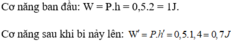
Phần cơ năng đã chuyển thành nội năng:
1. Do ma sát giữa bi và đá đã làm cho một phần cơ năng của hòn bi biến thành nội năng và tỏa nhiệt.
Và lượng cơ năng đã được chuyển hóa bằng độ biến thiên cơ năng của vật:\(\Delta W=W_1-W_2=mgh_1-mgh_2=mg\left(h_1-h_2\right)\)
2. chọn gốc thế năng tại mặt đất,
Công của lực cản bằng độ biến thiên cơ năng:
\(A=\Delta W=\dfrac{1}{2}mv^2-\left(mgz_0+\dfrac{1}{2}mv_0^2\right)\)
Vì một phần cơ năng của quả bóng đã chuyển hoá thành nội năng của bóng, sân và không khí:
∆ U = E 1 - E 2 = mg( h 1 - h 2 ) = 2,94 J
b)\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,02\cdot4^2=0,16J\)
\(W_t=mgz=0,02\cdot10\cdot1,6=0,32J\)
\(W=W_đ+W_t=0,16+0,32=0,48J\)
c)Độ cao cực đại:
\(h_{max}=\dfrac{W}{mg}=\dfrac{0,48}{0,02\cdot10}=2,4m\)
Vận tốc vạt khi chạm đất:
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot1,6}=4\sqrt{2}\)m/s
d)Cơ năng tại nơi \(W_đ=W_t\):
\(W'=W_đ+W_t=2W_đ=2\cdot\dfrac{1}{2}mv'^2=mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow0,48=mv'^2\Rightarrow v=\sqrt{\dfrac{0,48}{0,02}}=2\sqrt{6}\)m/s
Thế năng: \(W_t=W_đ=\dfrac{1}{2}\cdot0,02\cdot\left(2\sqrt{6}\right)^2=0,24J\)
Độ cao đạt được:
\(h'=\dfrac{W_t}{mg}=\dfrac{0,24}{0,02\cdot10}=1,2m\)
e)Độ biến thiên động năng:
\(A_c=\Delta W=\dfrac{1}{2}m\left(v_2^2-v_1^2\right)=\dfrac{1}{2}\cdot0,02\cdot\left(0^2-4^2\right)=-0,16J\)
Đáp án: D
Chọn mốc thế năng tại mặt tấm đá.
Cơ năng ban đầu:
W = P.h = 0,5.2 = 1J.
Cơ năng sau khi bi nảy lên:
W’ = P.h’ = 0,5.1,4 = 0,7J.
Phần cơ năng đã chuyển thành nội năng:
∆W = W – W’ = 1 – 0,7 = 0,3J.