Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)

ok, thanks nhưng dừng khoảng chừng là 2 giây, you lấy từ qanda

a) Tam giác ABC nhọn:
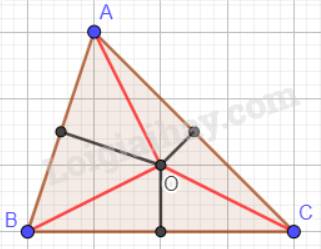
b) Tam giác ABC vuông tại A:
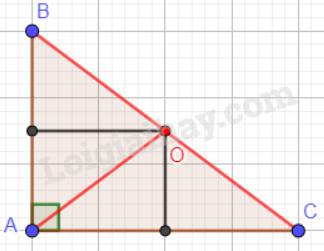
c) Tam giác ABC có góc A tù:
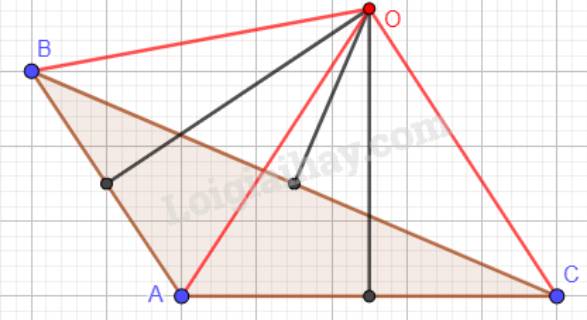

\(\Delta ABC\)có \(\widehat{A}=60^o\)\(\Rightarrow\widehat{B}+\widehat{C}=120^o\)
mà \(\widehat{B}=3.\widehat{C}\)\(\Rightarrow4.\widehat{C}=120^o\)\(\Rightarrow\widehat{C}=30^o\)\(\Rightarrow\widehat{B}=90^o\)
\(\Rightarrow\Delta ABC\)vuông tại B

a) Thấy ˆMAC=ˆMAB+ˆBAC=90o+ˆBAC=ˆCAN+ˆBAC=ˆBANMAC^=MAB^+BAC^=90o+BAC^=CAN^+BAC^=BAN^
Từ đây ta xét t/g MAC và BAN ta có:
=>MA=BA; AC=AN
=>ˆMAC=ˆBANMAC^=BAN^
=>ΔMAC=ΔBAN(c−g−c)⇒MC=BNΔMAC=ΔBAN(c−g−c)⇒MC=BN
đpcm.
b)
Ta gọi giao điểm của MC và BN là 1 điểm D
Ta có: ˆDBA=ˆDMA(ΔMAC=ΔBAN(c−g−c))DBA^=DMA^(ΔMAC=ΔBAN(c−g−c))
Nên ˆMBD+ˆBMD=ˆMBA+ˆDBA+ˆBMD=ˆMBA+ˆDMA+ˆBMD=ˆMBAMBD^+BMD^=MBA^+DBA^+BMD^=MBA^+DMA^+BMD^=MBA^
+ˆBMA=90o+BMA^=90o
Xét t/g MBD có ˆMBD+ˆBMD=90o⇒ˆBMD=90oMBD^+BMD^=90o⇒BMD^=90o
⇒BN⊥MC⇒BN⊥MC
Bổ sung D giao điểm nhé vào hình nha bn.
c) Ta giả sử như ABC đều cạnh 4cm (theo đề bài) thì sẽ có: AM=AC=AB=NA=4cm
Áp dụng định lý pi-ta-go ta có:
Cho t/g MAB và NAC thì MB=NC=4√2(cm)42(cm)
Khi ABC đều cạnh 4cm thì AMC = NAB là t/g vuông cân có góc ở đỉnh : 90o+60o=150o
=>ˆAMC=ˆACMAMC^=ACM^= (180o-150o):2=15o
Thì ˆMCB=ˆACB−ˆACM=60o−15o=45oMCB^=ACB^−ACM^=60o−15o=45o
Lại có ˆMAN=360o−90o−60o−90o=120oMAN^=360o−90o−60o−90o=120o
Vì t/gMAN cân tại A nên ˆAMNAMN^= (180o-120o) : 2 =30o
=> ˆCNM=30o+15o=45oCNM^=30o+15o=45o
=>ˆCNM=ˆMCBCNM^=MCB^
=> BC//MN ( so le trong)
đpcm.
Ta có: a2 + b2 = c2 nên tam giác ABC là tam giác vuông.
Chọn C