Một đa giác đều có góc ở mỗi đỉnh bằng α và nội tiếp đường tròn bán kính R thì có độ dài mỗi cạnh là:
A.R sinα
B. 2 R c o s α 2
C. R cos α / 2
D. 2R sinα
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
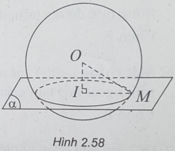
(h.2.58) Gọi I là hình chiếu của O lên ( α ) và M là điểm thuộc đường giao tuyến của ( α ) và mặt cầu S(O;R).
Tam giác OIM vuông tại I, ta có:
OM = R và OI = d
nên 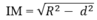

Chọn C.
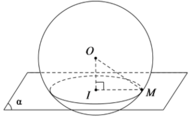
*) Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
*) Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên ![]()

Chọn C.
Gọi I là hình chiếu của O lên (α) và M là điểm thuộc đường giao tuyến của (α) và mặt cầu S(O; R).
Khi d < R thì mặt phẳng cắt mặt cầu (S) theo giao tuyến là đường tròn tâm I bán kính r = IM.
Xét tam giác OIM vuông tại I, ta có: OM = R và OI = d nên
![]()
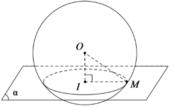

a, Ta đã chứng minh được: AE = b + c - a 2
=> AE = a + b + c - 2 a 2 = p – a
∆AIE có IE = EA.tan B A C ^ 2
= (p – a).tan B A C ^ 2
b, Chú ý: BI ⊥ FD và CI ⊥ E. Ta có:
B I C ^ = 180 0 - I B C ^ + I C D ^ = 180 0 - 1 2 A B C ^ + A C B ^
= 180 0 - 1 2 180 0 - B A C ^ = 90 0 + B A C ^ 2
Mà: E D F ^ = 180 0 - B I C ^ = 90 0 - α 2
c, BH,AI,CK cùng vuông góc với EF nên chúng song song => H B A ^ = I A B ^ (2 góc so le trong)
và K C A ^ = I A C ^ mà I A B ^ = I A C ^ nên H B A ^ = K C A ^
Vậy: ∆BHF:∆CKE
d, Do BH//DP//CK nên B D D C = H P P K mà DB = DF và CD = CE
=> H P P K = B F C E = B H C K => ∆BPH:∆CPK => B P H ^ = C P E ^
Lại có: B F P ^ = C E F ^ => ∆BPF:∆CEP (g.g)
mà B P D ^ = C P D ^ => PD là phân giác của B P C ^

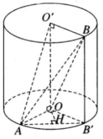
Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2


Nếu d < R thì giao tuyến của mặt phẳng α với mặt cầu S O ; R là đường tròn có bán kính bằng R 2 - d 2
Chọn: C
ĐÁP ÁN B
Giả sử A, B, C là ba đỉnh liên tiếp của đa giác đều.
Tam giác ABC cân tại B có góc ở đỉnh là α, góc ở đáy là 90 ° − α 2 .
Tam giác ABC nội tiếp đường tròn bán kính R nên a = 2 R sin 90 ° − α 2 = 2 R cos α 2