Cho phương trình z 2 + m z - 6 i = 0 . Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng m = ± ( a + b i ) ( a , b ∈ R ) . Giá trị a + 2 b là:
A. 0
B. 1
C. -2
D. -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Gọi z1; z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có: 
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
![]()
Suy ra: m2 = 5 - 12i
Do đó: m = ± ( 3 - 2i)
Vậy a = 3 ; b = -2 và a + 2b = -1

Chọn D
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
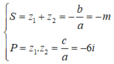
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
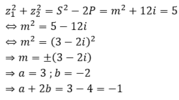

Chọn C.
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
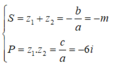
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:
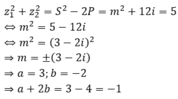

a: x^2+2xm+m^2=0
Khi m=5 thì pt sẽ là x^2+10x+25=0
=>x=-5
b: Thay x=-2 vào pt, ta được:
4-4m+m^2=0
=>m=2

a= 1; b= - 2(m-1) ; b'= -m+1; c=2m-5
a)
Xét: Δ'=b'2 - ac = (-m+1)2-(2m-5)= m2-2m+1-2m+5=m2-4m+6=m2-4m+4+2=(m-2)2+2
Vì (m-2)2≥0 nên Δ'=(m-2)2+2>0. Suy ra PT luôn có nghiệm.
b) Theo hệ thức Viet ta có:
S=x1+x2=\(\dfrac{-b}{a}\)=2(m-1)
Theo đề ra tổng 2 nghiệm bằng 6 nên:
2(m-1)=6 ⇔m=4
Vậy với m=4 thì PT có tổng 2 nghiệm bằng 6.

a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0

a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: 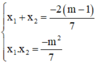
Khi đó:
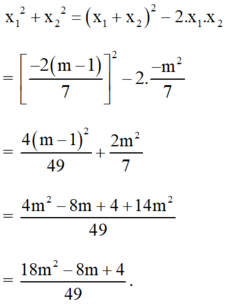
Chọn D
Gọi z1, z2 là hai nghiệm của phương trình đã cho
Theo Viet, ta có:
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có: