với những giá trị nào của m#0 thì hệ pt
mn - y = 2
3x +my =5
có nghiệm (x:y) thỏa mãn x+y= 1-\(\frac{m^2}{m^2+3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hàm số y=(m+6)x-7 đồng biến thì m+6>0
=>m>-6
b: Để hàm số y=(-k+9)x+100 nghịch biến thì -k+9<0
=>-k<-9
=>k>9
c: Để hai đồ thị hàm số y=12x+(5+m) và y=-3x+(3-m) cắt nhau tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}m+5=3-m\\12\ne-3\left(đúng\right)\end{matrix}\right.\)
=>m+5=3-m
=>2m=-2
=>m=-1

a) Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)
Hàm số đồng biến khi m – 1 > 0 hay m > 1.
Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.
b) Hàm số y = (5 – k)x + 1 là hàm số bậc nhất đối với x khi 5 – k ≠ 0 hay k ≠ 5 (**).
Hàm số nghịch biến khi 5 – k < 0 hay k > 5.
Kết hợp với điều kiện (**) ta được với k > 5 thì hàm số nghịch biến.

a: Thay x=0 và y=0 vào (d), ta được:
\(0\left(2-5m\right)+m-3=0\)
=>m-3=0
=>m=3
b: Để (d) tạo với trục Ox một góc nhọn thì 2-5m>0
=>5m<2
=>\(m< \dfrac{2}{5}\)
Để (d) tạo với trục Ox một góc tù thì 2-5m<0
=>5m>2
=>\(m>\dfrac{2}{5}\)
c: Thay x=0 và \(y=\dfrac{2}{3}\) vào (d), ta được:
\(0\left(2-5m\right)+m-3=\dfrac{2}{3}\)
=>\(m-3=\dfrac{2}{3}\)
=>\(m=\dfrac{2}{3}+3=\dfrac{11}{3}\)
d: thay \(x=\dfrac{1}{2};y=0\) vào (d), ta được:
\(\dfrac{1}{2}\left(2-5m\right)+m-3=\dfrac{2}{3}\)
=>\(1-\dfrac{5}{2}m+m-3=\dfrac{2}{3}\)
=>\(-\dfrac{3}{2}m-2=\dfrac{2}{3}\)
=>\(-\dfrac{3}{2}m=2+\dfrac{2}{3}=\dfrac{8}{3}\)
=>\(m=-\dfrac{8}{3}:\dfrac{3}{2}=-\dfrac{16}{9}\)

a) Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)
Hàm số đồng biến khi m – 1 > 0 hay m > 1.
Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.
b) Hàm số y = (5 – k)x + 1 là hàm số bậc nhất đối với x khi 5 – k ≠ 0 hay k ≠ 5 (**).
Hàm số nghịch biến khi 5 – k < 0 hay k < 5.
Kết hợp với điều kiện (**) ta được với k < 5 thì hàm số nghịch biến.
a, y= 5x - (2-x)k = 5x - 2k + k.x = (5+k)x - 2k
Vậy hàm số có hệ số a= 5+k. Khi đó:
+ Hàm số đồng biến a > 0 ⇔ 5 + k > 0 ⇔ k > -5
+ Hàm số nghịch biến a < 0 ⇔ 5 + k < 0 ⇔ k < -5.

a,khi m-1>=0 thi ham so dong bien tuc m>=1
b,khi 5-k<=0 thi ham so nghich bien tuc k>=5
a) Khi m - 1 \(\ge\)0 thì hàm số đồng biến tức m \(\ge\)1
b) Khi 5 - k \(\le\)0 thì hàm số nghịch biến tức k \(\ge\)5

Đáp án D
Với mọi cặp vectơ ![]()
Dấu bằng xảy ra khi và chỉ khi ![]() hay hai vectơ này vuông góc. Điều đó tương đương với điều kiện:
hay hai vectơ này vuông góc. Điều đó tương đương với điều kiện:
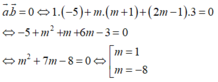
Nếu chúng ta suy nghĩ sai là: ‘‘sin ( a → , b → ) đạt giá trị lớn nhất khi và chỉ khi góc giữa hai vectơ đó lớn nhất’’ thì khi đó góc giữa hai vectơ bằng 180o, do đó tồn tại số k âm sao cho:
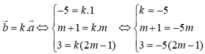
Hệ này vô nghiệm và dẫn đến ta chọn đáp án là D.

Hàm số y = (m + 6)x – 7 đồng biến khi hệ số a > 0
Ta có: m + 6 > 0 ⇔ m > -6
Vậy với m > -6 thì hàm số y = (m + 6)x – 7 đồng biến

Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)
Hàm số đồng biến khi m – 1 > 0 hay m > 1.
Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.
\(\int^{mx-y=2}_{3x+my=5}\Leftrightarrow\int^{y=mx-2}_{3x+m.\left(mx-2\right)=5}\Leftrightarrow\int^{y=mx-2}_{3x+m^2x-2m=5}\)
*3x+m2x-2m=5
<=>x.(3+m2)=5+2m
<=>x=\(\frac{5+2m}{3+m^2}\left(3+m^2>0\right)\)
\(\Rightarrow y=m.\left(\frac{5+2m}{3+m^2}\right)-2=\frac{5m+2m^2}{3+m^2}-\frac{6+2m^2}{3+m^2}=\frac{5m-6}{3+m^2}\)
=>\(x+y=\frac{5+2m}{3+m^2}+\frac{5m-6}{3+m^2}=\frac{7m-1}{m^2+3}\)
=>\(\frac{7m-1}{m^2+3}=1-\frac{m^2}{m^2+3}\Leftrightarrow\frac{7m-1}{m^2+3}=\frac{m^2+3}{m^2+3}-\frac{m^2}{m^2+3}\)
=>7m-1=m2+3-m2
=>7m-1=3
=>m=4/7
Vậm m=4/7