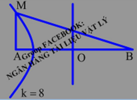
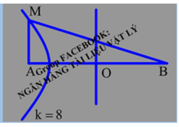
Tại mặt thoáng của một chất lỏng có hai nguồn phát sóng kết hợp A và B cách nhau 8 cm. Cho A, B dao động điều hòa, cùng pha, theo phương vuông góc với mặt chất lỏng. Bước sóng của sóng trên mặt chất lỏng là 1 cm. Gọi M, N là hai điểm thuộc mặt chất lỏng sao cho MN = 4 cm và AMNB là hình thang cân. Để trên đoạn MN có đúng 5 điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình thang có thể là:
A. 18 5 c m 2 .
B. 9 3 c m 2 .
C. 9 5 c m 2 .
D. 18 3 c m 2 .




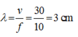
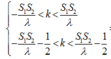
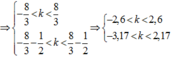
Đáp án A
Số điểm dao động với biên độ cực đại trên AB
- A B λ ≤ k ≤ A B λ ⇔ - 8 ≤ k ≤ 8
Để diện tích AMNB là lớn nhất thì M phải nằm trên cực đại ứng với k=-2
d 1 - d 2 = - 2 k λ = - 2 c m .
Mặc khác d 1 2 = A H 2 + M H 2 d 2 2 = B H 2 + M H 2 ⇒ d 1 + d 2 = B H 2 - A H 2 2 = 16 c m
Ta tính được d 1 = 7 c m từ đó suy ra M H = 2 5 c m .
Diện tích hình thang S A M N B = 1 2 A B + M N M H = 18 5 c m 2 .