Cho tam giác ABC, đường thẳng d song song BC cắt hai cạnh AB và AC tại M và N sao cho AM = 4cm, MB = 8cm và BC = 36cm. Tính MN?
A. 10cm
B. 8cm
C. 12cm
D. 7cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do M nằm giữa A và B nên: AB = AM + MB = 13 + 11 = 24 cm
Theo hệ quả định lí Ta let ta có:
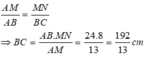
Chọn đáp án C


a
Do \(MN//BC\) nên theo định lý Thales ta có:\(\frac{AN}{NC}=\frac{AM}{MB}=\frac{MN}{BC}\)
\(\Rightarrow\frac{8}{NC}=\frac{3}{2}\Rightarrow NC=\frac{16}{3}\)
Áp dụng định Pythagoras ta có:\(AM^2+AN^2=MN^2\Rightarrow MN=\sqrt{AM^2+AN^2}=10\)
Mà \(\frac{AM}{MB}=\frac{MN}{BC}\Rightarrow\frac{3}{2}=\frac{10}{BC}\Rightarrow BC=\frac{20}{3}\)
b
Hạ \(NH\perp BC;MG\perp BC\)
Áp dụng định lý Pythagoras vào tam giác ABC ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AB^2=\sqrt{BC^2-AC^2}\Rightarrow AB=\sqrt{10-\left(\frac{16}{3}\right)^2-8^2}=\frac{2\sqrt{17}}{3}\)
Bạn áp dụng định lý Ta Lét ( do ND//AB ) rồi tính được ND
Diện tích tam giác vuông NCD sẽ tính bằng \(\frac{NC\cdot ND}{2}\) ( do đã biết được ND và NC )
Lại có \(S_{NCD}=\frac{NH\cdot CD}{2}\) rồi tính được NH.
Do NH=MG nên tính được diện tích hình bình hành BMND.Hướng là thế đấy,bạn làm tiếp nha,mik nhác quá:(

a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).

Vì tam giác ABC cân tại A nên AB = AC = 10cm
Vì MN// BC, theo định lí Ta – let ta có:
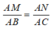
Mà AB = AC nên AM = AN = 4cm
Suy ra :

Chọn đáp án C

vẽ hình(tự vẽ)
a) Xét △ABC có MN // BC(gt) ,theo định lí Ta-lét ta có:
\(\dfrac{AM}{MB}\)=\(\dfrac{AN}{NC}\) hay \(\dfrac{6}{4}\)=\(\dfrac{8}{NC}\)⇒NC=\(\dfrac{8.4}{6}\)=5,3(cm)
Ta có: AB=AM+BM=6+4=10(cm)
AC=AN+NC=8+5,3=13,3(cm)
Áp dụng định lý Py-ta-go vào △ABC vuông tại A ta có:
BC=\(\sqrt{AB^2+AC^2}\)=\(\sqrt{10^2+13,3^2}\)=\(\sqrt{276,89}\)=16,6(cm)
Xét △ABC có MN // BC,theo hệ quả định lí Ta -lét ta có:
\(\dfrac{AM}{AB}\)=\(\dfrac{MN}{BC}\)hay \(\dfrac{6}{10}\)=\(\dfrac{MN}{16,6}\)⇒MN=\(\dfrac{16,6.6}{10}\)=9,96(cm)
b)
Điểm M nằm giữa A và B nên: AB = AM + MB = 4 + 8 = 12cm
Áp dụng hệ quả định lí Ta let ta có;
Chọn đáp án C