Cho hàm số f ( x ) = - 1 4 x có đồ thị (C) và các điểm M (0; 4); P (4; −1); Q (−4; 1); A (8; −2); O (0; 0). Có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm số (C).
A. 4
B. 3
C. 2
D. 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = 3 x ta được:
+) Với M (1; 1), thay x = 1 ; y = 1 ta được 1 = 3 . 1 ⇔ 1 = 3 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = 3 . 0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (−1; −3), thay x = − 1 ; y = − 3 ta được − 3 = 3 . ( − 1 ) ⇔ − 3 = − 3 (luôn đúng) nên P ∈ (C)
+) Với Q (3; 9), thay x = 3 ; y = 9 ta được 9 = 3 . 3 ⇔ 9 = 9 (luôn đúng) nên Q ∈ (C)
+) Với M (−2; 6), thay x = − 2 ; y = 6 ta được 6 = 3 . ( − 2 ) ⇔ 6 = − 6 (vô lý) nên A (C)
Vậy có ba điểm thuộc đồ thị (C) trong số các điểm đã cho.
Đáp án cần chọn là: B

a: Thay x=10 và y=-15 vào f(x), ta được:
10m-20=-15
=>10m=5
hay m=1/2

Bài 1 :
Với x = 1 thì y = 4.1 = 4
Ta được \(A\left(1;4\right)\) thuộc đồ thị hàm số y = f(x) = 4x
Đường thẳng OA là đồ thị hàm số y = f(x) = 4x
y x 4 3 2 1 1 2 3 4 -1 -2 -3 -4 y=4x A
a) Ta có : \(f\left(2\right)=4\cdot2=8\)
\(f\left(-2\right)=4\cdot\left(-2\right)=-8\)
\(f\left(4\right)=4\cdot4=16\)
\(f\left(0\right)=4\cdot0=0\)
b) +) y = -1 thì \(4x=-1\) => \(x=-\frac{1}{4}\)
+) y = 0 thì 4x = 0 => x = 0
+) y = 2,5 thì 4x = 2,5 => \(4x=\frac{5}{2}\)=> x = \(\frac{5}{8}\)
Bài 2 :
a) Vẽ tương tự như bài 1
b) Thay \(M\left(-2,6\right)\)vào đths y = -3x ta có :
y =(-3)(-2) = 6
=> Điểm M thuộc đths y = -3x
c) Thay tung độ của P là 5 vào đồ thị hàm số y = -3x ta có :
=> 5 = -3x => \(x=-\frac{5}{3}\)
Vậy tọa độ của điểm P là \(P\left(-\frac{5}{3};5\right)\)

a)
f(0) = 2 . 0 - 2 = -2
f(1) = 2.1 - 2 = 0
f(-1)= 2.(-1) - 2 = -4
b) Thay tọa độ A,B vào phương trình đồ thị hàm số ta có :
A : -2 = 2. 0 - 2 đúng=> A \(\in\)u= 2x -2
B: 1 = 2 . (-1) - 2 sai => B \(\in\)y =2x - 2
c) \(C\in y=2x-2\Rightarrow2=2m-2\Leftrightarrow m=2\)

+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 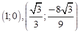 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
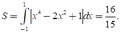
Chọn D.

Xác định hệ số a, biết rằng đồ thị của hàm số y=ax đi qua điểm A(6;2).Điểm B(-9;3), điểm C(7;-2) có thuộc đồ thị hàm số không ? Tìm trên đồ thị của hàm số điểm D có hoành độ bằng -4,điểm E có tung độ bằng 2
Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = - 1 4 x ta được:
+) Với M (0; 4), thay x = 0; y = 4 ta được 4 = - 1 4 .0 ⇔ 4 = 0 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = - 1 4 .0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (4; −1), thay x = 4 ; y = − 1 ta được −1 = - 1 4 . 4 ⇔ 1 = −1 (luôn đúng) nên P ∈ (C)
+) Với Q (−4; 1), thay x = − 4 ; y = 1 ta được 1 = - 1 4 .(−4) ⇔ 1 = 1 (luôn đúng) nên Q ∈ (C)
+) Với A (8; −2), thay x = 8 ; y = − 2 ta được −2 = - 1 4 .8 ⇔ −2 = −2 (luôn đúng) nên A ∈
Đáp án cần chọn là: A