Cho đường thẳng d : y = − 2 x – 4 . Gọi A, B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.
A. 2
B. 4
C. 3
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

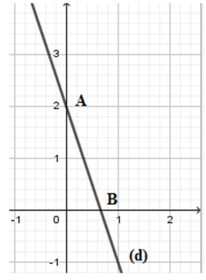
B (x; 0) là giao điểm của d với trục hoành nên 0 = − 3 x + 2 ⇔ x = 2 3 B 2 3 ; 0
A (0; y) là giao điểm của d với trục tung nên y = − 3 . 0 + 2 ⇔ y = 2 ⇒ A ( 0 ; 2 )
Suy ra O A = | 2 | = 2 ; O B = 2 3 = 2 3
Vì tam giác OAB vuông tại O nên SOAB = O A . O B 2 = 2. 2 3 2 = 2 3 (đvdt)
Đáp án cần chọn là: D

a: Phương trình hoành độ giao điểm là:
2x=-3x+5
=>5x=5
=>x=1
Thay x=1 vào y=2x, ta được:
\(y=2\cdot1=2\)
Vậy: M(1;2)
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-3x+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{5}{3}\end{matrix}\right.\)
Vậy: A(5/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-3\cdot0+5=5\end{matrix}\right.\)
Vậy: B(0;5)
O(0;0); A(5/3;0); B(0;5)
=>\(OA=\sqrt{\left(\dfrac{5}{3}-0\right)^2+\left(0-0\right)^2}=\dfrac{5}{3}\)
\(OB=\sqrt{\left(0-0\right)^2+\left(5-0\right)^2}=5\)
Vì A,B là giao điểm của (d): y=-3x+5 với trục Ox và trục Oy nên ΔOAB vuông tại O
=>\(S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{5}{3}\cdot5=\dfrac{25}{6}\)
M(1;2); O(0;0); A(5/3;0)
\(OA=\sqrt{\left(\dfrac{5}{3}-0\right)^2+\left(0-0\right)^2}=\dfrac{5}{3}\)
\(OM=\sqrt{\left(1-0\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(MA=\sqrt{\left(\dfrac{5}{3}-1\right)^2+\left(0-2\right)^2}=\dfrac{2\sqrt{10}}{3}\)
Xét ΔOAM có \(cosAOM=\dfrac{OA^2+OM^2-AM^2}{2\cdot OA\cdot OM}=\dfrac{\sqrt{5}}{5}\)
=>\(sinAOM=\sqrt{1-\left(\dfrac{\sqrt{5}}{5}\right)^2}=\dfrac{2}{\sqrt{5}}\)
\(S_{AOM}=\dfrac{1}{2}\cdot OA\cdot OM\cdot sinAOM\)
\(=\dfrac{1}{2}\cdot\sqrt{5}\cdot\dfrac{5}{3}\cdot\dfrac{2}{\sqrt{5}}=\dfrac{5}{3}\)

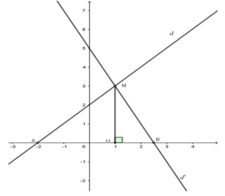
Xét phương trình hoành độ giao điểm của d 1 v à d 2
x + 2 = − 2 x + 5 ⇔ x = 1 ⇒ y = 3 ⇒ d 1 ∩ d 2 t ạ i M ( 1 ; 3 )
Gọi H là chân đường vuông góc kẻ từ M tới Ox. Suy ra MH = 3
d ∩ Ox tại A (−2; 0) ⇒ OA = 2
d’ ∩ Ox tại B 5 2 ; 0 ⇒ O B = 5 2
A B = O A + O B = 2 + 5 2 = 9 2
SMAB = 1 2 AB.MH = . 1 2 . 3 9 2 = 27 4 (đvdt)
Đáp án cần chọn là: D

2: Tọa độ điểm A là:
\(\left\{{}\begin{matrix}y_A=0\\-x_A+1=0\end{matrix}\right.\Leftrightarrow A\left(1;0\right)\)
Tọa độ điểm B là:
\(\left\{{}\begin{matrix}x_B=0\\y_B=-0+1=1\end{matrix}\right.\)
Vậy: B(0;1)
\(S_{OAB}=\dfrac{OA\cdot OB}{2}=\dfrac{1}{2}\)
3: Vì (d')//(d) nên a=-1
Vậy: (d'): y=-x+b
Thay x=0 và y=-2 vào (d'), ta được:
b-0=-2
hay b=-2

Do A là giao (d) với trục tung \(\Rightarrow x_A=0\Rightarrow y_A=\left(m-2\right).0+m-1=m-1\)
\(\Rightarrow OA=\left|y_A\right|=\left|m-1\right|\)
Do B là giao (d) với trục hoành
\(\Rightarrow y_B=0\Rightarrow\left(m-2\right)x_B+m-1=0\Rightarrow x_B=-\dfrac{m-1}{m-2}\) (với \(m\ne2\))
\(\Rightarrow OB=\left|x_B\right|=\left|\dfrac{m-1}{m-2}\right|\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}.\left|m-1\right|.\left|\dfrac{m-1}{m-2}\right|=1\)
\(\Rightarrow\left(m-1\right)^2=2\left|m-2\right|\) (1)
TH1: \(m>2\)
(1) \(\Leftrightarrow m^2-2m+1=2m-4\Rightarrow m^2-4m+5=0\) (vô nghiệm)
TH2: \(m< 2\)
\(\left(1\right)\Leftrightarrow m^2-2m+1=2\left(2-m\right)\Leftrightarrow m^2+2m-3=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\) (thỏa mãn)
A (x; 0) là giao điểm của d với trục hoành nên 0 = − 2 x ⇔ x = − 2 ⇒ A ( − 2 ; 0 )
B (0; y) là giao điểm của d với trục tung nên y = − 2 . 0 – 4 ⇔ y = − 4 ⇒ B ( 0 ; − 4 )
Suy ra O A = | − 2 | = 2 ; O B = | − 4 | = 4
Vì tam giác )AB vuông tại O nên S O A B = O A . O B 2 = 2.4 2 = 4 (đvdt)
Đáp án cần chọn là: B