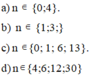5n+3 chia hết cho 2n+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2017
2) Ta có : 2n - 2 = 2(n - 1) chia hết cho n - 1
Nên với mọi giá trị của n thì 2n - 2 đều chia hết cho n - 1
3) Ta có : 5n - 1 chia hết chi n - 2
=> 5n - 10 + 9 chia hết chi n - 2
=> 5(n - 2) + 9 chia hết chi n - 2
=> n - 2 thuộc Ư(9) = {1;3;9}
Ta có bảng :
| n - 2 | 1 | 3 | 9 |
| n | 3 | 5 | 11 |
4 tháng 7 2017
1) Ta có : 2n + 3 chia hết cho 3n + 1
<=> 6n + 9 chia hết cho 3n + 1
<=> 6n + 2 + 7 chia hết cho 3n + 1
=> 7 chia hết cho 3n + 1
=> 3n + 1 thuộc Ư(7) = {1;7}
Ta có bảng :
| 3n + 1 | 1 | 7 |
| 3n | 0 | 6 |
| n | 0 | 2 |
Vậy n thuộc {0;2}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 9 2023
a, 2n + 3 ⋮ n ( n \(\ne\) 0)
3 ⋮ n
n \(\in\) Ư(3) = { -3; -1; 1; 3}
b, 2n + 16 ⋮ n + 1 ( n \(\ne\) -1)
2(n + 1) + 14 ⋮ n + 1
14 ⋮ n + 1
n + 1 \(\in\) { -14; -7; -2; -1; 1; 2; 7; 14}
n \(\in\) {-15; - 8; -3; -2; 0; 1; 6; 13}
c, 5n + 12 ⋮ n - 3 (n \(\ne\) 3)
5.(n - 3) + 27 ⋮ n - 3
27 ⋮ n -3
n - 3 \(\in\) {-27; -9; -3; -1; 1; 3; 9; 27}
n \(\in\) {-24; -6; 0; 2; 6; 12; 30}
KV
27 tháng 9 2023
a) (2n + 3) ⋮ n khi 3 ⋮ n
⇒ n ∈ {-3; -1; 1; 3}
b) 2n + 16 = 2n + 2 + 14 = 2(n + 1) + 14
Để (2n + 16) ⋮ (n + 1) thì 14 ⋮ (n + 1)
⇒ n + 1 ∈ Ư(14) = {-14; -7; -2; -1; 1; 2; 7; 14}
⇒ n ∈ {-15; -8; -3; -2; 0; 1; 6; 13}
c) Ta có:
5n + 12 = 5n - 15 + 27 = 5(n - 3) + 27
Để (5n + 12) ⋮ (n - 3) thì 27 ⋮ (n - 3)
⇒ n - 3 ∈ Ư(27) = {-27; -9; -3; -1; 1; 3; 9; 27}
⇒ n ∈ {-24; -6; 0; 2; 4; 6; 12; 30}
OS
1
17 tháng 2 2020
a.n+3 chia hết cho n-1
suy ra: n-1+4 chia hết cho n-1
mà n-1 chia hết cho n-1
nên n-1 thuộc Ư(4)={1;-1;2;-2;4;-4}
ta có các trường hợp sau:
TH1: n-1=1 nên n=2
TH2: n-1=-1 nên n=0
TH3: n-1=2 nên n=3
TH4: n-1=-2 nên n=-1
TH5: n-1=4 nên n=5
TH6:n-1=-4 nên n=-3
TT
1
NN
1 tháng 2 2017
\(a,5n-1⋮3n-7\)
\(15n-3⋮3n-7\)
\(5\left(3n-7\right)+32⋮3n-7\)
\(\Rightarrow32⋮3n-7\)
\(\Rightarrow3n-7\)là ước của \(32\)
\(\Rightarrow3n-7\in\left\{-32;-16;-8;-4;-2;-1;1;2;4;8;16;32\right\}\)
\(\Rightarrow3n\in\left\{-25;-9;-1;3;5;6;8;9;11;15;23;39\right\}\)
\(\Rightarrow n\in\left\{-3;1;2;3;5;13\right\}\left(n\in Z\right)\)
\(b,7n+3⋮2n+5\)
\(14n+6⋮2n+5\)
\(7\left(2n+5\right)-29⋮2n+5\)
\(\Rightarrow29⋮2n+5\)
\(\Rightarrow2n+5\in\left\{-29;-1;1;29\right\}\)
\(\Rightarrow2n\in\left\{-34;-6;-4;24\right\}\)
\(\Rightarrow n\in\left\{-17;-3;-2;12\right\}\)
NY
0
20 tháng 12 2018
a) ta có: 3n + 1 chia hết cho 2n - 3
=> 6n + 2 chia hết cho 2n - 3
6n - 9 + 11 chia hết cho 2n - 3
3.(2n-3) + 11 chia hết cho 2n - 3
mà 3.(2n-3) chia hết cho 2n - 3
=> 11 chia hết cho 2n - 3
=>...
bn tự làm tiếp nha
20 tháng 12 2018
b) ta có: 5n - 3 chia hết cho 2n + 1
=> 10n - 6 chia hết cho 2n + 1
10n + 5 - 11 chia hết cho 2n + 1
5.(2n+1) - 11 chia hết cho 2n + 1
...
13 tháng 11 2016
a) 5n + 6 chia hết cho 5n + 1
5n + 1 + 5 chia hết cho 5n + 1
=> 5 chia hết cho 5n + 1
=> 5n + 1 thuộc Ư(5) = {1 ; -1 ; 5 ; -5}
Xét 4 trường hợp, ta có '
5n + 1 = 1 => 5n = 0 => n = 0
5n + 1 = -1 => 5n = -2 => n = -2/5
5n + 1 = 5 => 5n = 4 => n = 4/5
5n + 1 = -5 => 5n = -6 => n = -6/5
b)
2n + 3 chia hết cho 3n + 1
3(2n + 3 ) chia hết cho 3n + 1
6n + 9 chia hết cho 3n + 1
6n + 2 + 7 chia hết cho 3n + 1
2(3n + 1) + 7 chia hết cho 3n + 1
=> 7 chia hết cho 3n + 1
=> 3n + 1 thuộc Ư(7) = {1 ; -1 ; 7 ; -7}
Còn lại làm giống bài a nha