Một vật dao động điều hòa với tần số góc ω . Chu kì dao động của vật được tính bằng công thức
A. T = ω 2 π
B. T = 2 π ω
C. 1 ω 2 π
D. T = 2 π ω
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dao động điều hòa là dao động có toạ độ là một hàm sin hoặc côsin theo thời gian dạng x = Acos( ω t + φ ) hoặc
x = Asin( ω t + φ )
Trong đó chu kì: là khoảng thời gian ngắn nhất để vật lặp lại một trạng thái dao động (trạng thái cũ gồm: vị trí cũ và chiều chuyển động cũ) ⇒ T = ∆ t N = 2 π ω

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B

Chọn đáp án A.
Vận tốc góc ω = π rad/s
=> Tần số góc của dao động điều hòa tương ứng là ω = π (rad/s)

Xem giản đồ Fre-nen (H.5.6G)
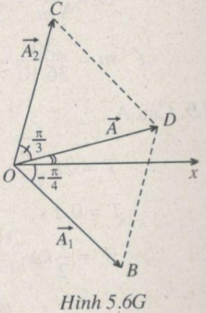
A 1 → + A 2 → = 6cm ⇒ ∆ COD cân
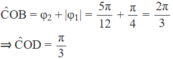
Pha ban đầu của dao động tổng hợp là :
![]()
A → = A 1 → = A 2 →

Đáp án A
Biểu thức li độ của vật dao động điều hòa theo thời gian là
![]()
Chọn B
Dao động điều hòa là dao động có toạ độ là một hàm sin hoặc côsin theo thời gian dạng x = A cos ω t + φ hoặc x = A sin ω t + φ
Trong đó chu kì: là khoảng thời gian ngắn nhất để vật lặp lại một trạng thái dao động (trạng thái cũ gồm: vị trí cũ và chiều chuyển động cũ) ⇒ T = Δ t N = 2 π ω