Phương trình dao động của vật có dạng x = A . cos 2 ω t + π 4 . Chọn kết luận mô tả đúng dao động của vật:
A. Vật dao động có tần số góc ω
B. Vật dao động có biên độ A, tần số góc ω
C. Vật dao động có biên độ A
D. Vật dao động có biên độ 0,5A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Biến đổi:
![]()
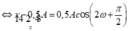
Đặt X=x-0,5A phương trình mô tả dao động với biên độ 0,5A.

ü Đáp án D
+ Biến đổi
x = A cos 2 ω t + π 4 = 0 , 5 A + 0 , 5 A cos 2 ω + π 2 ⇔ x - 0 , 5 A ⏟ X = 0 , 5 A cos 2 ω + π 2
Đặt X = x – 0,5A → phương trình mô tả dao động với biên độ 0,5A

Đáp án D
Biến đổi x = A c os 2 ω t + π 4 = 0 , 5 A + 0 , 5 A c os 2 ω + π 2 ⇔ x − 0 , 5 A ⏟ x = 0 , 5 A c os 2 ω + π 2
Đặt X = x - 0,5 => phương trình mô tả dao động với biên độ 0,5A

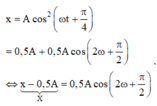
Đặt X = x – 0,5A → phương trình mô tả dao động với biên độ 0,5A.
Đáp án D

Đáp án D
Biến đổi
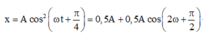
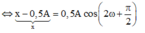
Đặt X = x - 0,5A phương trình mô tả dao động với biên độ 0,5A

Đáp án D
Biến đổi


Đặt X = x - 0,5A phương trình mô tả dao động với biên độ 0,5A

Đáp án C
Phương trình li độ của vật dao động điều hòa được xác định bằng biểu thức x = A cos ω t + φ

Vật đi qua vị trí cân bằng theo chiều dương :
\(\left\{{}\begin{matrix}x_0=0\\v_0>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A\cdot cos\varphi=0\\-\omega A\cdot sin\varphi>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cos\varphi=0\\sin\varphi< 0\end{matrix}\right.\)
\(\Leftrightarrow\varphi=\dfrac{-\pi}{2}\)
\(x=Acos\left(\omega t-\dfrac{\pi}{2}\right)\)
=> B