OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
2 tháng 11 2019
Tìm khẳng định sai trong các khẳng định sau: A.  lim x → - 2 x 2 + 5 - 3 = 0 B.  lim x → - ∞ - 3 x 3 + 2 x + 5 = - ∞ C.  lim x → + ∞ x 2 + 2 x + 3 = + ∞ D.  lim x → 2 ...
Đọc tiếp

Tìm khẳng định sai trong các khẳng định sau:

A.  lim x → - 2 x 2 + 5 - 3 = 0

B.  lim x → - ∞ - 3 x 3 + 2 x + 5 = - ∞

C.  lim x → + ∞ x 2 + 2 x + 3 = + ∞

D.  lim x → 2 2 x + 3 x - 1 = 7

#Mẫu giáo
1
CM
Cao Minh Tâm
2 tháng 11 2019

Đáp án B

Ta có  lim x → - ∞ - 3 x 3 + 2 x + 5 = + ∞

Đúng(0)
AV
A8_ Võ Thị Thương
16 tháng 5 2023

Biết lim x -> +∞ f(x) = M ;lim x -> +∞ g(x) = 0 Chọn khẳng định đúng? A. Lim x -> +∞ f(x)/g(x)= +∞ B. Lim x -> +∞ = f(x)/g(x)= -∞ C. Lim x -> +∞ f(x)/g(x)=0 D. Limx -> +∞ [g(x).f(x)]=0
#Toán lớp 11
0
AV
A8_ Võ Thị Thương
16 tháng 5 2023

Xin đa tạ 

Đúng(0)
PT
Pham Trong Bach
27 tháng 12 2019
Cho hàm số y = f(x) có       lim x → + ∞ f ( x ) = 3   và lim   x → - ∞ f ( x ) = - 3 Khẳng định nào sau đây là khẳng định đúng? A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3 C. Đồ thị hàm số đã cho...
Đọc tiếp

Cho hàm số y = f(x) có       lim x → + ∞ f ( x ) = 3   và lim   x → - ∞ f ( x ) = - 3 Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang

B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3

C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3

D. Đồ thị hàm số đã cho không có tiệm cận ngang
#Toán lớp 12
1
CM
Cao Minh Tâm
27 tháng 12 2019

Đáp án C.

Ta có: 

=> y = 3, y = -3 là hai tiệm cận ngang.

Đúng(0)
PT
Pham Trong Bach
26 tháng 3 2019

Trong các khẳng định sau đây, khẳng định nào sai?

    A. |x| ≥ 0, ∀ x          B. |x| + x ≥ 0, ∀ x

    C. |x| ≥ a, ⇒ x ≥ a          D. |x| - x ≥ 0, ∀ x
#Toán lớp 10
1
CM
Cao Minh Tâm
26 tháng 3 2019

A, B, D đúng theo các tính chất của giá trị tuyệt đối, do đó C sai.

Đáp án: C

Đúng(0)
PT
Pham Trong Bach
16 tháng 8 2019
Cho hàm số f ( x ) = 2 - x ( x - 2 ) 2 k h i   x ≠ 2 3 k h i   x = 2 . Tìm khẳng định sai trong các khẳng định sau đây? A. Hàm số liện tục trên R.  B. Hàm số liện tục trên khoảng (-∞ ; 2).  C. Hàm số gián đoạn tại x = 2.  D. Hàm số liện tục trên khoảng...
Đọc tiếp

Cho hàm số f ( x ) = 2 - x ( x - 2 ) 2 k h i   x ≠ 2 3 k h i   x = 2 . Tìm khẳng định sai trong các khẳng định sau đây?

A. Hàm số liện tục trên R. 

B. Hàm số liện tục trên khoảng (-∞ ; 2). 

C. Hàm số gián đoạn tại x = 2. 

D. Hàm số liện tục trên khoảng (2 ; +∞).
#Toán lớp 11
1
CM
Cao Minh Tâm
16 tháng 8 2019

Chọn A.

- Với mọi x ≠ 2 thì hàm số liên tục.

- Tại điểm x = 2 ta có f(2) = 3.

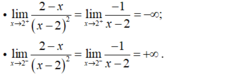
Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)

→ Do đó hàm số gián đoạn tại x = 2.

Đúng(0)
PT
Pham Trong Bach
14 tháng 1 2017
Cho hàm số y = f x  có l i m   f x x → − ∞ = 2   v à   l i m   f x x → + ∞ = − 2.  Khẳng định nào sau đây là khẳng định đúng? A. Đồ thị hàm số đã cho không có tiệm cận ngang B. Đồ thị hàm số đã cho có hai tiệm cận ngang y = 2   v ...
Đọc tiếp

Cho hàm số y = f x  có l i m   f x x → − ∞ = 2   v à   l i m   f x x → + ∞ = − 2.  Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận ngang

B. Đồ thị hàm số đã cho có hai tiệm cận ngang y = 2   v à   y = − 2

C. Đồ thị hàm số đã cho có hai tiệm cận đứng  x = 2   v à  x = − 2

D. Đồ thị hàm số đã cho không có tiệm cận
#Mẫu giáo
1
CM
Cao Minh Tâm
14 tháng 1 2017

Đáp án B

Đúng(0)
MN
maianh nguyễn
25 tháng 2 2020
Chọn khẳng định đúng trong các khẳng định sau: Câu 1: A.Nếu lim|\(u_n\)|=+oo, thì lim\(u_n\)= +oo B. Nếu lim|\(u_n\)|=+oo, thì lim\(u_n\)=-oo C.Nếu lim\(u_n\)=0, thì lim|\(u_n\)|=0 D.C.Nếu lim\(u_n\)=-a, thì lim|\(u_n\)|=a Câu 2: (I). f(x)=\(\frac{\sqrt{x+1}}{x-1}\) liên tục với mọi x≠1 (II). f(x)=sinx liên tục trên R (III). f(x)=\(\frac{\left|x\right|}{x}\)liên tục tại x=1 A. Chỉ (I) đúng B. Chỉ (I) va (II) C, Chỉ (I) và (III) D. Chỉ (II) va...
Đọc tiếp

Chọn khẳng định đúng trong các khẳng định sau:

Câu 1:

A.Nếu lim|\(u_n\)|=+oo, thì lim\(u_n\)= +oo B. Nếu lim|\(u_n\)|=+oo, thì lim\(u_n\)=-oo

C.Nếu lim\(u_n\)=0, thì lim|\(u_n\)|=0 D.C.Nếu lim\(u_n\)=-a, thì lim|\(u_n\)|=a

Câu 2:

(I). f(x)=\(\frac{\sqrt{x+1}}{x-1}\) liên tục với mọi x≠1

(II). f(x)=sinx liên tục trên R

(III). f(x)=\(\frac{\left|x\right|}{x}\)liên tục tại x=1

A. Chỉ (I) đúng B. Chỉ (I) va (II) C, Chỉ (I) và (III) D. Chỉ (II) va (III)
#Toán lớp 11
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2020

Câu 1: đáp án C đúng (đáp án A và B hiển nhiên sai, đáp án D chỉ đúng khi a không âm)

Câu 2: (I) sai, vì với \(x< -1\) hàm ko xác định nên ko liên tục

(II) đúng do tính chất hàm sin

(III) đúng do \(\lim\limits_{x\rightarrow1}\frac{\left|x\right|}{x}=\frac{\left|1\right|}{1}=f\left(1\right)\)

Vậy đáp án D đúng

Đúng(0)
PT
Pham Trong Bach
3 tháng 12 2017
1.    Cho phương trình x - 2 m x + m - 2 = 0 .Chỉ ra khẳng định sai trong các khẳng định sau: A.  K h i   m = 3   t h ì   x 1 - x 2 = 4 2 B.  K h i   m = 2   t h ì   x 1 - x 2 = 4 C.  K h i   m = 1   t h ì   x ...
Đọc tiếp

1.    Cho phương trình x - 2 m x + m - 2 = 0 .

Chỉ ra khẳng định sai trong các khẳng định sau:

A.  K h i   m = 3   t h ì   x 1 - x 2 = 4 2

B.  K h i   m = 2   t h ì   x 1 - x 2 = 4

C.  K h i   m = 1   t h ì   x 1 - x 2 = 2 2

D. có giá trị của m để x 1 = x 2 .
#Toán lớp 10
1
CM
Cao Minh Tâm
3 tháng 12 2017

* Với m= 3 thì phương trình đã cho trở thành:  x2 – 6x + 1= 0.

Phương trình này có 2 nghiệm x 1 = 3 + 2 2 ;   x 2 = 3 - 2 2  nên x 1 - x 2 = 4 2

 * Với m= 2 thì phương trình đã cho trở thành:  x2 – 4x = 0.

Phương trình này có 2 nghiệm là x1 =0 và x2 = 4 nên |x1 – x2| = 4

* Với m= 1 thì phương trình đã cho trở thành:  x2 – 2x - 1= 0.

Phương trình này có 2 nghiệm x 1 = 1 + 2 ;   x 2 = 1 - 2 nên  x 1 - x 2 = 2 2

* Phương trình đã cho có:

∆ ' = m 2 - m - 2 = m 2 - m + 2 = m 2 - 2 . 1 2 . m + 1 4 + 7 4 = m - 1 4 2 + 7 4 > 0   ∀ m

Do đó, không có giá trị nào của m để ∆’ = 0 hay không có giá trị nào của m để phương trình đã cho có nghiệm kép.

Chọn D.

Đúng(0)
QT
Quoc Tran Anh Le
Giáo viên
24 tháng 9 2023

Trong các khẳng định sau, khẳng định nào là mệnh đề, khẳng định nào là mệnh đề chứa biến

a) \(3 + 2 > 5\)

b) \(1 - 2x = 0\)

c) \(x - y = 2\)

d) \(1 - \sqrt 2  < 0\)
#Toán lớp 10
1
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023

Các khẳng định là mệnh đề là:

a) \(3 + 2 > 5\)

d) \(1 - \sqrt 2  < 0\)

Các khẳng định là mệnh đề chứa biến là:

b) \(1 - 2x = 0\)

c) \(x - y = 2\)

Đúng(0)
PT
Pham Trong Bach
25 tháng 5 2018
Cho hàm số  y = - 2 x - 1 k h i   x < - 1 1 + 2 x - x 2 k h i   - 1 ≤ x ≤ 2 1 k h i   x > 2 . Tìm khẳng định sai trong các khẳng định sau  A. Hàm số liên tục trên khoảng (-∞ ; -1).  B. Hàm số liên tục trên khoảng...
Đọc tiếp

Cho hàm số  y = - 2 x - 1 k h i   x < - 1 1 + 2 x - x 2 k h i   - 1 ≤ x ≤ 2 1 k h i   x > 2 . Tìm khẳng định sai trong các khẳng định sau 

A. Hàm số liên tục trên khoảng (-∞ ; -1). 

B. Hàm số liên tục trên khoảng (-1 ; +∞). 

C. Hàm số liên tục tại điểm x 0   =   2 . 

D. Hàm số liên tục tại điểm  x 0   =   - 1 .  
#Toán lớp 11
1
CM
Cao Minh Tâm
25 tháng 5 2018

- Ta có:

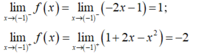
Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)

- Suy ra: 

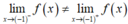
Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)

nên hàm số gián đoạn tại điểm  x 0   =   - 1 .

Chọn D

Đúng(0)
PT
Pham Trong Bach
28 tháng 10 2017
Tìm khẳng định sai trong các khẳng định sau đây:A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;B. Đồ thị hàm số sau có hai tiệm cận đứng y = 3 x 2 - 2 x + 5 x 2 + x - 7 C. Hàm số  y = 3 x - 2 3 x + 4  luôn nghịch biến;D. Hàm số ...
Đọc tiếp

Tìm khẳng định sai trong các khẳng định sau đây:

A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;

B. Đồ thị hàm số sau có hai tiệm cận đứng y = 3 x 2 - 2 x + 5 x 2 + x - 7

C. Hàm số  y = 3 x - 2 3 x + 4  luôn nghịch biến;

D. Hàm số f x = - 2 x   với   x ≥ 0 sin x 3   với   x < 0

không có đạo hàm tại x = 0.
#Toán lớp 12
1
CM
Cao Minh Tâm
28 tháng 10 2017

Đáp án: B.

Xét f(x) = x 3  + m x 2  + x - 5

Vì 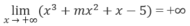Giải sách bài tập Toán 12 | Giải sbt Toán 12

và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP