Với a b, là 2 số dương tùy ý thì log a 3 b 2 bằng
A. 3 log a + 1 2 log b
B. 2 log a + 3 log b
C. 3 log a + 1 2 log b
D. 3 log a + 2 log b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

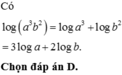

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)

Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)


\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)

a) \(\log_a\left(a^2b\right)=\log_aa^2+\log_ab=2.\log_aa+\log_ab=2.1+2=4\)
b) \(\log_a\dfrac{a\sqrt{a}}{b\sqrt[3]{a}}=\log_a\left(a\sqrt{a}\right)-\log_a\left(b\sqrt[3]{b}\right)=\log_aa^{\dfrac{3}{2}}-\log_ab^{\dfrac{4}{3}}=\dfrac{3}{2}.\log_aa-\dfrac{4}{3}\log_ab=\dfrac{3}{2}.1-\dfrac{4}{3}.2=-\dfrac{7}{6}\)
c) \(\log_a\left(2b\right)+\log_a\left(\dfrac{b^2}{2}\right)=\log_a2+\log_ab+\log_ab^2-\log_a2=\log_ab+2\log_ab=3\log_ab=3.2=6\)
a: \(=log_aa^2+log_ab=2+2=4\)
b: \(log_a\left(\dfrac{a\sqrt{a}}{b\sqrt[3]{b}}\right)=log_aa^{\dfrac{3}{2}}-log_ab^{\dfrac{4}{3}}\)
=3/2-4/3*2
=3/2-8/3
=9/6-16/6=-7/6
c: \(log_a\left(2b\right)+log_a\left(\dfrac{b^2}{2}\right)\)
\(=log_a\left(2b\cdot\dfrac{b^2}{2}\right)=log_a\left(b^3\right)=3\cdot2=6\)

a: \(log_49=\dfrac{log9}{log4}=\dfrac{log3^2}{log2^2}=\dfrac{2\cdot log3}{2\cdot log2}=\dfrac{log3}{log2}=\dfrac{b}{a}\)
b: \(log_612=\dfrac{log12}{log6}=\dfrac{log2^2+log3}{log2+log3}=\dfrac{2\cdot log2+log3}{log2+log3}\)
\(=\dfrac{2a+b}{a+b}\)
c: \(log_56=\dfrac{log6}{log5}=\dfrac{log\left(2\cdot3\right)}{log\left(\dfrac{10}{2}\right)}=\dfrac{log2+log3}{log10-log2}\)
\(=\dfrac{a+b}{1-a}\)
a: l o g 4 9 = l o g 9 l o g 4 = l o g 3 2 l o g 2 2 = 2 ⋅ l o g 3 2 ⋅ l o g 2 = l o g 3 l o g 2 = b a log 4 9= log4 log9 = log2 2 log3 2 = 2⋅log2 2⋅log3 = log2 log3 = a b b: l o g 6 12 = l o g 12 l o g 6 = l o g 2 2 + l o g 3 l o g 2 + l o g 3 = 2 ⋅ l o g 2 + l o g 3 l o g 2 + l o g 3 log 6 12= log6 log12 = log2+log3 log2 2 +log3 = log2+log3 2⋅log2+log3 = 2 a + b a + b = a+b 2a+b c: l o g 5 6 = l o g 6 l o g 5 = l o g ( 2 ⋅ 3 ) l o g ( 10 2 ) = l o g 2 + l o g 3 l o g 10 − l o g 2 log 5 6= log5 log6 = log( 2 10 ) log(2⋅3) = log10−log2 log2+log3 = a + b 1 − a = 1−a a+b