Cho hàm số y=f(x) có đồ thị như hình vẽ bên
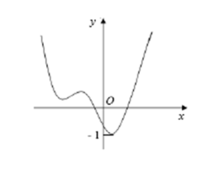
Tìm số điểm cực trị của hàm số y = 2 f x − 3 f x
A. 6
B. 5
C. 4
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.

Đáp án C

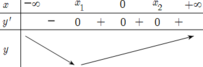
Khi đó hàm số y=f(x) đạt cực tiểu tại x = x 1 hay hàm số y=f(x) có 1 điểm cực trị.

Đáp án B.
f ' (x) đổi dấu 1 lần, suy ra hàm số y = f(x) có 1 điểm cực trị.

Đáp án B
Nhìn vào đồ thị hàm số ta thấy có một giá trị của x (gải sử x = a) để y’=0 và không có giá trị nào của x làm y’ không xác định. Mặt khác y' đổi dấu từ dương sang âm khi đi qua x = a do vậy x = a là một điểm cực trị của hàm số y=f(x).
Ta chọn B
Đáp án D
Phương pháp giải:
Tính đạo hàm của hàm số và tìm nghiệm của phương trình y'=0 dựa vào bài toán tương giao và đồ thị hàm số y=f(x) =>Số điểm cực trị của hàm số cần tìm.
Lời giải:
xét hàm số
Dựa vào đồ thị hàm số y = f(x), ta thấy:
Phương trình (1) có 3 nghiệm phân biệt (vì hàm số y = f(x) có 3 điểm cực trị).
Phương trình (2) vô nghiệm vì đường thẳng y = log 2 3 ln 3 ln 2 < − 1 không cắt ĐTHS.
Vậy phương trình g'(x) = 0 có 3 nghiệm phân biệt hay hàm số đã cho có 3 điểm cực trị.