Cho hàm số f x = x 3 − 3 x 2 + 5. Tiếp tuyến của đồ thị hàm số tại điểm − 1 ; 1 thuộc đồ thị hàm số có phương trình là :
A. y = 3 − 2 x
B. y = 9 x + 10
C. y = 1 + 3 x
D. y = − 3 x + 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2021
\(f\left(3\right)=\dfrac{3}{2}\) ; \(f\left(\dfrac{3}{2}\right)=\dfrac{6}{5}\) ; \(f'\left(x\right)=\dfrac{1}{\left(x+1\right)^2}\Rightarrow f'\left(3\right)=\dfrac{1}{10}\) ; \(f'\left(\dfrac{3}{2}\right)=\dfrac{4}{25}\)
\(g\left(3\right)=f\left(f\left(3\right)\right)=f\left(\dfrac{3}{2}\right)=\dfrac{6}{5}\)
\(g'\left(x\right)=f'\left(f\left(x\right)\right).f'\left(x\right)\Rightarrow g'\left(3\right)=f'\left(f\left(3\right)\right).f'\left(3\right)=f'\left(\dfrac{3}{2}\right).\dfrac{1}{10}=\dfrac{2}{125}\)
Tiếp tuyến:
\(y=\dfrac{2}{125}\left(x-3\right)+\dfrac{6}{5}\)
Hoặc đơn giản nhất là tìm thẳng hàm g(x) ra \(g\left(x\right)=\dfrac{2\left(\dfrac{2x}{x+1}\right)}{\dfrac{2x}{x+1}+1}\) rút gọn rồi viết pttt
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
CM
24 tháng 5 2017
Chọn đáp án D
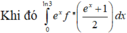
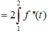
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy
CM
27 tháng 9 2018
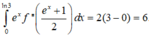
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2021
Thay \(x=1\Rightarrow2f\left(2\right)+3f\left(2\right)=10\Rightarrow f\left(2\right)=5\)
Đạo hàm 2 vế giả thiết:
\(-6f'\left(5-3x\right)+3f'\left(x+1\right)=2x+4\)
Thay \(x=1\)
\(-6f'\left(2\right)+3f'\left(2\right)=6\Rightarrow f'\left(2\right)=-2\)
Phương trình tiếp tuyến:
\(y=-2\left(x-2\right)+5=-2x+9\)
CM
22 tháng 8 2017
Đáp án A
Với x=0 thay vào hai vế của đẳng thức f 2 1 + 2 x = x − f 3 1 − x ta có f 2 1 = − f 3 1 .
Đạo hàm hai vế của đẳng thức đã cho, ta có:
4 f 1 + 2 x . f ' 1 + 2 x = 1 + 3 f 2 1 − x . f ' 1 − x → x = 0 2 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1
Ta có hệ phương trình sau: f 2 1 = − f 3 1 4 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1
⇔ f 2 1 f 1 + 1 = 0 4 f 1 . f ' 1 = 1 + 3 f 2 1 . f ' 1 ⇔ f 1 = − 1 f ' 1 = − 1 7
Vậy tiếp tuyến cần tìm là
y
=
f
'
1
.
x
−
1
+
f
1
=
−
1
7
x
−
1
−
1
⇔
y
=
−
1
7
x
−
6
7
27 tháng 4 2022
có:
+) đạo hàm của f(x) = f'(x) = 3x2
+) phương trình tiếp tuyến là : y= f'(x).(x-x0) + f(x0)
=> y = 3x2.(x-1) + 13 + 3 = 3x3 - 3x2 + 4
Đáp án B
Ta có y ' = 3 x 3 − 6 x .
Hệ số góc của tiếp tuyến tại điểm (-1;1) là k = y ' − 1 = 9
Do đó phương trình tiếp tuyến là y = 9 x + 10.