Cho hàm số y = 1 3 x 3 - 2 x 2 + 2 x + 1 C . Biết đồ thị (C) có hai tiếp tuyến cùng vuông góc với đường thẳng d : y = x . Gọi h là khoảng cách giữa hai tiếp tuyến đó. Tính h.
A. h = 2
B. h = 4 2 3
C. h = 2 3
D. h = 2 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ giả thiết suy ra tiếp tuyến có hệ số góc bằng -1
Hai tiếp điểm có hoành độ là nghiệm của phương trình y ' x 0 = - 1
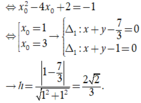
Chọn C.

Đáp án D
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) là: y = f'(x0).(x - x0) + y0
Cách giải:
![]()
Tiếp tuyến của (C) vuông góc với đường thẳng d: y = x nên tiếp tuyến có hệ số góc k = -1
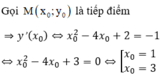
![]()
=> Phương trình tiếp tuyến
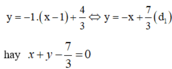
![]()
=> Phương trình tiếp tuyến
![]()
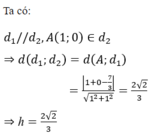

\(y'=3x^2+6x-6\)
Tiếp tuyến vuông góc đường thẳng đã cho nên có hệ số góc thỏa mãn:
\(k.\left(-\dfrac{1}{18}\right)=-1\Rightarrow k=18\)
\(\Rightarrow3x^2+6x-6=18\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=9\\x=-4\Rightarrow y=9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=18\left(x-2\right)+9\\y=18\left(x+4\right)+9\end{matrix}\right.\)

\(y=x^3-3x^2+2x+2\Rightarrow y'=3x^2-6x+2\)
Vi \(\Delta\perp d:y=x-3\Rightarrow y'=-1\Leftrightarrow3x^2-6x+2=-1\)
\(\Rightarrow x=1\Rightarrow y=1-3+2+2=2\)
\(\Rightarrow\Delta:y=-1\left(x-1\right)+2\)

a.
\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)
b.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)

\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được
Đáp án D