Hàm số y = f(x) có đạo hàm trên ℝ \ − 2 ; 2 , có bảng biến thiên như sau:
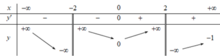
Gọi k, l lần lượt là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 f x − 2018
Tính k + l
A. k + l = 3
B. k + l = 4
C. k + l = 5
D. k + l = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựa vào bảng biến thiên ta thấy rằng f’(-2)=f’(1)=f’(3)=0.
f’(x)đổi dấu khi qua hai điểm x=-2; x=3 và f’(x) không đổi dấu khi qua điểm x=1 nên hàm số y=f(x) có hai diểm cực trị.
Đáp án A

Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.

Đáp án D
Ta có y ' = f 1 - x + 2018 x + 2019 ' = 1 - x ' . f ' 1 - x + 2018 = - f ' 1 - x + 2018
= - x 3 - x . g 1 - x - 2018 + 2018 = - x 3 - x . g 1 - x mà g 1 - x < 0 ; ∀ x ∈ ℝ
Nên y ' < 0 ⇔ - x 3 - x . g 1 - x < 0 ⇔ x 3 - x . g 1 - x > 0 ⇔ x 3 - x < 0 ⇔ [ x > 3 x < 0
Khi đó, hàm số y = f 1 - x + 2018 x + 2019 nghịch biến trên khoảng 3 ; + ∞

Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
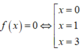
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
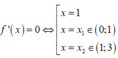
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
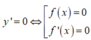
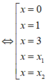
Ta có BXD của y' như sau
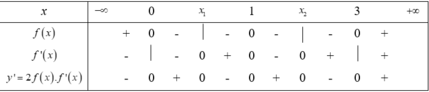
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.

Ta có ![]()
![]()
Suy ra số nghiệm của phương trình g'(x) = 0 chính là số giao điểm giữa đồ thị của hàm số f'(x) và parapol ![]()
Dựa vào đồ thị ta suy ra 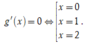
Bảng biến thiên
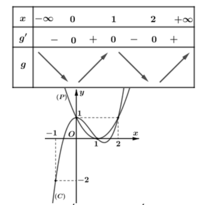
Dựa vào bảng biến thiên ta thấy g(x) đạt cực đại tại x = 1
Chọn C.
Chọn C