Cho nửa đường tròn đường kính AB=2R,vẽ tiếp tuyến Ax của đường tròn đó,M là điểm di động trên nửa đường tròn ,BM cắt Ax tại C.Xác định vị trí điểm M để 2BM +BC đạt giá trị nhỏ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

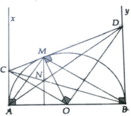
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB

Tự vẽ hình nhé !
Dễ dàng chỉ ra được \(\widehat{COD}=90^o\).
Khi đó \(\Delta COD\) vuông tại \(O\) có \(OM\perp CD\) nên theo hệ thức lượng trong tam giác vuông có :
\(CM.MD=MO^2=R^2\)
Theo BĐT Cô - si thì : \(CD=CM+MD\ge2.\sqrt{CM.MD}=2\sqrt{R^2}=2R\)
Dấu "=" xảy ra khi M là điểm chính giữa của cung AB.

a/
Xét tg vuông OAC và tg vuông OMC có
OA=OM=R
OC chung
=> tg OAC = tg OMC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AOC}=\widehat{MOC}=\dfrac{\widehat{AOM}}{2}\)
Tương tự ta cũng có
tg OBD = tg OMD \(\Rightarrow\widehat{BOD}=\widehat{MOD}=\dfrac{\widehat{BOM}}{2}\)
\(\Rightarrow\widehat{MOC}+\widehat{MOD}=\widehat{COD}=\dfrac{\widehat{AOM}}{2}+\dfrac{\widehat{BOM}}{2}=\dfrac{180^o}{2}=90^o\)
b/
AB+BD nhỏ nhất khi \(M\equiv B\)