Hàm số y = f(x) có đạo hàm f ' x = − x − 1 2 − 1 , ∀ x ∈ ℝ . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên ( − ∞ ; 1 ) .
B. Hàm số đồng biến trên (0;1)
C. Hàm số nghịch biến trên − ∞ ; + ∞ .
D. Hàm số đồng biến trên 1 ; + ∞ .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có f ' x = x 2 + 3 ≥ 0 ∀ x ∈ R .
Vậy hàm số đồng biến trên .

g’(x)=2f(x).f’(x)-4.f’(x)=2f’(x).[f(x)-2]
Từ đồ thị trên của y=f’(x) suy ra BBT của y=f(x). Suy ra max f(x)=f(1)=1
Do đó f(x)-2< 0, x ϵ R
g’(x)=0→f’(x)=0→x= -1 hoặc x=1.
Lập bảng biến thiên suy ra min g(x)= -3
Đáp án A

Đáp án D
Ta thấy f'(x) =0 tại x=3,x=1 nhưng chỉ đổi dấu qua x = 3 nên hàm số có đúng 1 cực trị

Đáp án C
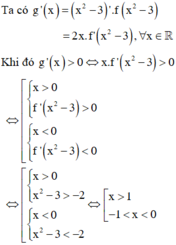
Suy ra hàm số đồng biến trên khoảng (-1;0) và 1 ; + ∞
Đáp án C
Từ giả thiết em có f ' x = − x − 1 2 − 1 < 0 , ∀ x ∈ ℝ . Hàm số f(x) luôn nghịch biến trên − ∞ ; + ∞ .