Cho l i m x → ∞ f x = 2 2018 . Tính l i m x → ∞ f x - 1 f x + 1 .
A. 2 2018 - 1
B. 4 2018 + 1
C. 4 2018 - 1
D. 2 2018 + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

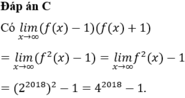

Lời giải:
Theo ý c, số dư khi chia đa thức $f(x)$ cho $(x-2)(x-3)$ sẽ không vượt quá bậc 2. Do đó số dư có dạng \(ax+b\)
Đặt \(f(x)=(x-2)(x-3)(x^2-1)+ax+b\) (*)
Theo định lý Bezout về số dư đa thức, số dư của $f(x)$ khi chia cho $x-2$ và $x-3$ là \(f(2); f(3)\)
Do đó: \(f(2)=5; f(3)=7\)
Thay vào (*) ta có:
\(\left\{\begin{matrix} f(2)=0+2a+b=5\\ f(3)=0+3a+b=7\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=2\\ b=1\end{matrix}\right.\)
Vậy \(f(x)=(x-2)(x-3)(x^2-1)+2x+1\)
\(\Leftrightarrow f(x)=x^4-5x^3+5x^2+7x-5\)

Để \(f\left(x\right)=\left(ax+b\right)^2\)
\(\Leftrightarrow x^2-\left(2m+1\right)x+m^2+1=\left(ax+b\right)^2\)
\(\Leftrightarrow x^2-\left(2m+1\right)x+\left(m^2+1\right)=a^2x^2+2abx+b^2\)
Đồng nhất hệ số ta được :
\(\left\{{}\begin{matrix}a^2=1\\2ab=-\left(2m+1\right)\\b^2=m^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\pm1\\2ab=-2m-1\\b^2=m^2+1\end{matrix}\right.\)
Với \(a=1\Rightarrow\left\{{}\begin{matrix}2b=-2m-1\\b^2=m^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{4}\\b=-\dfrac{5}{4}\end{matrix}\right.\)
Với \(a=-1\Rightarrow\left\{{}\begin{matrix}-2b=-2m-1\\b^2=m^2+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{4}\\b=\dfrac{5}{4}\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{4}\)

Bài 1:
Từ P(x) = 3x2+8x-4 = -4
=> 3x2+8x = 0
x(3x+8) = 0
=> x = 0 3x+8 = 0
=> x = 0 3x = 8
=> x = 8/3
Bài 2 :
Ta có x = -1 là nghiệm của đa thức f(x) = 2x2-x+m
=> f(-1) = 2(-1)2-(-1)+m = 0
=> 2+1+m = 0
=> 3+m = 0
m = 0-3
m = -3

Bài 2 (sửa lại đề)
Cho hai đa thức:
P(x)=x2+2mx+m2
Q(x)=x2+(2m+1)+m2
Tìm m để P(x)=Q(x)

Câu a thì dài, câu b thì ngắn. Xin giải câu b trước để đi ngủ
b) Giải:
Vì \(f\left(x_1.x_2\right)=f\left(x_1\right).f\left(x_2\right)\) nên:
\(f\left(4\right)=f\left(2.2\right)=f\left(2\right).f\left(2\right)=10.10=100\)
\(f\left(16\right)=f\left(4.4\right)=f\left(4\right).f\left(4\right)=100.100=10000\)
\(f\left(32\right)=f\left(16.2\right)=f\left(16\right).f\left(2\right)=10000.10=100000\)
Vậy \(f\left(32\right)=100000\)

a.
f(2)-3f(2+1)=2*22
f(2) -3f*3=2*4
f(2)-9f=8
f(2)=8+9f
b.
f(-5)-3f(-5+1)=2*(-5)2
f(-5)-3f(-4)=2*25
f(-5)-(-12)f=50
f(-5)+12f=50
f(-5)=50-12f
c.
f(-2)-3f(-2+1)=2*(-2)2
f(-2)-3f(-1)=2*4
f(-2)-(-3)f=8
f(-2)+3f=8
f(-2)=8-3f
Mình vẫn chưa biết đúng hay sai nữa nha

Vì f(x) chia x+2 dư 10 nên f(x) -10 chia hết cho x+2
Theo Bezout ta có :
f(-2) - 10 = 0
=> f(-2) = 0
Cmtt f(2) = 22
Lại có : f(x) = -5x(x2 - 4) + ax+b (*)
Thay x = -2 vào (*) ta được:
f(-2) = -2a+b = 10
Thay x = 2 vào (*) ta được :
f(2) = 2a+b = 22
Giải bất phương trình \(\left\{{}\begin{matrix}-2a+b=10\\2a+b=22\end{matrix}\right.\)
Suy ra a= 3 ; b= 16
Vậy f(x) = -5x(x2-4)+3x+16