Biết sina+ cosa = a 2 . Hỏi giá trị của sin4a + cos4a bằng bao nhiêu?
A. 1
B. 0,5
C. -1
D. 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2020
\(A=\frac{\left(1+cos2x\right)}{cos2x}.tanx=\frac{\left(1+2cos^2x-1\right)}{cos2x}.\frac{sinx}{cosx}=\frac{2cos^2x.sinx}{cos2x.cosx}=\frac{2sinx.cosx}{cos2x}=\frac{sin2x}{cos2x}=tan2x\)
\(B=\frac{1+2sin2a.cos2a-1+2sin^22a}{1+2sin2a.cos2a+2cos^22a-1}=\frac{2sin2a\left(sin2a+cos2a\right)}{2cos2a\left(sin2a+cos2a\right)}=\frac{sin2a}{cos2a}=tan2a\)
\(C=\frac{2sina.cosa+sina}{1+2cos^2a-1+cosa}=\frac{sina\left(2cosa+1\right)}{cosa\left(2cosa+1\right)}=\frac{sina}{cosa}=tana\)
PT
1
CM
16 tháng 6 2017
Ta có ( sin a + cos a ) 2 = 1 + sin2a ⇒ 1/2 = 1 + sin2a. Vậy sin2a = (-1)/2
Đáp án: C
PH
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Chia cả tử và mẫu cho \(cosa\)
\(D=\dfrac{\dfrac{cosa}{cosa}+\dfrac{sina}{cosa}}{\dfrac{cosa}{cosa}-\dfrac{sina}{cosa}}=\dfrac{1+tana}{1-tana}=\dfrac{1+\dfrac{1}{2}}{1-\dfrac{1}{2}}=3\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2019
3/
\(cos4A+cos4B+cos4C=2cos\left(2A+2B\right).cos\left(2A-2B\right)+2cos^22C-1\)
\(=2cos2C.cos\left(2A-2B\right)+2cos^22C-1\)
\(=2cos2C\left(cos\left(2A-2B\right)+cos2C\right)-1\)
\(=2cos2C\left(cos\left(2A-2B\right)+cos\left(2A+2B\right)\right)-1\)
\(=4cos2A.cos2B.cos2C-1\Rightarrow\left\{{}\begin{matrix}a=-1\\b=4\end{matrix}\right.\)
4/
\(cos^2A+cos^2B+cos^2C=\frac{1}{2}+\frac{1}{2}cos2A+\frac{1}{2}+\frac{1}{2}cos2B+\frac{1}{2}+\frac{1}{2}cos2C\)
\(=\frac{3}{2}+\frac{1}{2}\left(cos2A+cos2B+cos2C\right)\)
\(=\frac{3}{2}+\frac{1}{2}\left[2cos\left(A+B\right).cos\left(A-B\right)+2cos^2C-1\right]\)
\(=1+\frac{1}{2}\left(-2cosC.cos\left(A-B\right)+2cos^2C\right)\)
\(=1-cosC\left(cos\left(A-B\right)-cosC\right)\)
\(=1-cosC\left(cos\left(A-B\right)+cos\left(A+B\right)\right)\)
\(=1-2cosA.cosB.cosC\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2019
1/ \(sinA+sinB+sin2\frac{C}{2}=2sin\frac{A+B}{2}cos\frac{A-B}{2}+2sin\frac{C}{2}cos\frac{C}{2}\)
\(=2cos\frac{C}{2}.cos\frac{A-B}{2}+2cos\frac{A+B}{2}.cos\frac{C}{2}=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)\)
\(=4cos\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}\Rightarrow\left\{{}\begin{matrix}a=0\\b=4\end{matrix}\right.\)
2/ \(sin4A+sin4B+sin4C=2sin\left(2A+2B\right)cos\left(2A-2B\right)+2sin2C.cos2C\)
\(=-2sin2C.cos\left(2A-2B\right)+2sin2C.cos2C\)
\(\)\(=2sin2C\left(cos2C-cos\left(2A-2B\right)\right)\)
\(=-4sin2C.sin\left(C+A-B\right)sin\left(C-A+B\right)\)
\(=-4sin2A.sin2B.sin2C\Rightarrow\left\{{}\begin{matrix}a=0\\b=-4\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 5 2020
\(A=2sin2x.cos2x.cos4x=sin4x.cos4x=\frac{1}{2}sin8x\)
\(B=sin^4x+cos^6x-6sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-8sin^2x.cos^2x\)
\(=1-2\left(2sinx.cosx\right)^2=1-2sin^22x=cos4x\)
\(C=\frac{cos2a+1-2cos^22a}{2sin2a.cos2a+sin2a}=\frac{\left(1-cos2a\right)\left(2cos2a+1\right)}{sin2a\left(2cos2a+1\right)}=\frac{1-cos2a}{sin2a}\)
\(=\frac{1-\left(1-2sin^2a\right)}{2sina.cosa}=\frac{2sin^2a}{2sina.cosa}=\frac{sina}{cosa}=tana\)
\(D=\frac{2cos3a.cos2a+cos3a}{2sin3a.cos2a+sin3a}=\frac{cos3a\left(2cos2a+1\right)}{sin3a\left(2cos2a+1\right)}=\frac{cos3a}{sin3a}=cot3a\)
\(E=\frac{1}{2}-\frac{1}{2}cos\left(\frac{\pi}{4}+x\right)-\frac{1}{2}+\frac{1}{2}cos\left(\frac{\pi}{4}+x\right)\)
\(=\frac{1}{2}\left[cos\left(\frac{\pi}{4}+x\right)-cos\left(\frac{\pi}{4}-x\right)\right]=-sin\frac{\pi}{4}.sinx=-\frac{\sqrt{2}}{2}sinx\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2020
\(A=cos^2a+cos^2b+2cosa.cosb+sin^2a+sin^2b+2sina.sinb\)
\(=cos^2a+sin^2a+cos^2b+sin^2b+2\left(cosa.cosb+sina.sinb\right)\)
\(=2+2cos\left(a-b\right)=2+2cos\frac{\pi}{3}=3\)
\(\left(cosa+sina\right)^2=\frac{36}{25}\Leftrightarrow1+2sina.cosa=\frac{36}{25}\)
\(\Rightarrow sin2a=\frac{36}{25}-1=\frac{11}{25}\)
\(cos2a=cos^2a-sin^2a=\left(cosa-sina\right)\left(cosa+sina\right)>0\)
\(\Rightarrow cos2a=\sqrt{1-sin^22a}=\frac{6\sqrt{14}}{25}\)
Chọn B.
Ta có: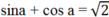
Nên (sina + cosa)2 =2 hay sin2a + cos2a + 2 sina.cosa = 2
Suy ra sina.cosa = ½.
Khi đó: sin4a + cos4a = (sin2a + cos2a)2 - 2sin2a.cos2a = 1 - 2.(1/2)2 = ½.